Underwater and Underground Explosions Simulation and Analysis Package

Categories: Abaqus, Acoustics, CEL and Eulerian, Concrete structure, Course, Explosion, Finite Element, Fracture & Failure Analysis, FSI and CFD, Ice, Jh2 and Jhb model, Steel structure, Structures

Underwater and Underground Explosions Simulation and Analysis Package

Peyman Karampour

Level

All Levels
Duration

8 hours 47 minutes
Last Updated

November 8, 2025
Certificate

Certificate of completion

28 people watching this product now!

This package includes 20 detailed tutorials that comprehensively explain underwater and underground explosions using various methods such as CEL, acoustic, and CONWEP.
The course covers a wide range of simulations, including ice damage, CFDST structures, floating structures, water explosion shocks, concrete dams, concrete slabs, soil craters, concrete gravity dams, hulls, marine structures, sandwich structures, steel piles, concrete piled-raft structures, pipelines, and tunnels.
This package will provide all that you need about the underwater and underground explosion, including all material data like JWL, EOS, JH2, JC damage, Mohr-Coulomb, ductile and shear damage, Water, air, and ...

About Course

Introduction to Underwater and Underground Explosions: Simulation and Analysis

1. Overview

Explosions occurring in confined or dense media such as water and soil differ significantly from those in the air. The interaction between the explosive energy and the surrounding medium creates complex physical phenomena involving shock wave propagation, fluid-structure interaction, and material deformation. Understanding and simulating these events are critical for applications in defense engineering, mining, civil infrastructure protection, and marine systems.

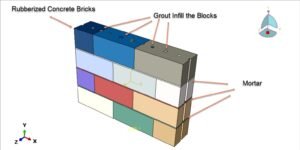
This package includes 20 detailed tutorials that comprehensively explain underwater and underground explosions using various methods such as CEL, acoustic, and CONWEP. The course covers a wide range of simulations, including ice damage, CFDST structures, floating structures, water explosion shocks, concrete dams, concrete slabs, soil craters, concrete gravity dams, hulls, marine structures, sandwich structures, steel piles, concrete piled-raft structures, pipelines, and tunnels.

2. Nature of the Explosions

Underwater Explosions (UNDEX):
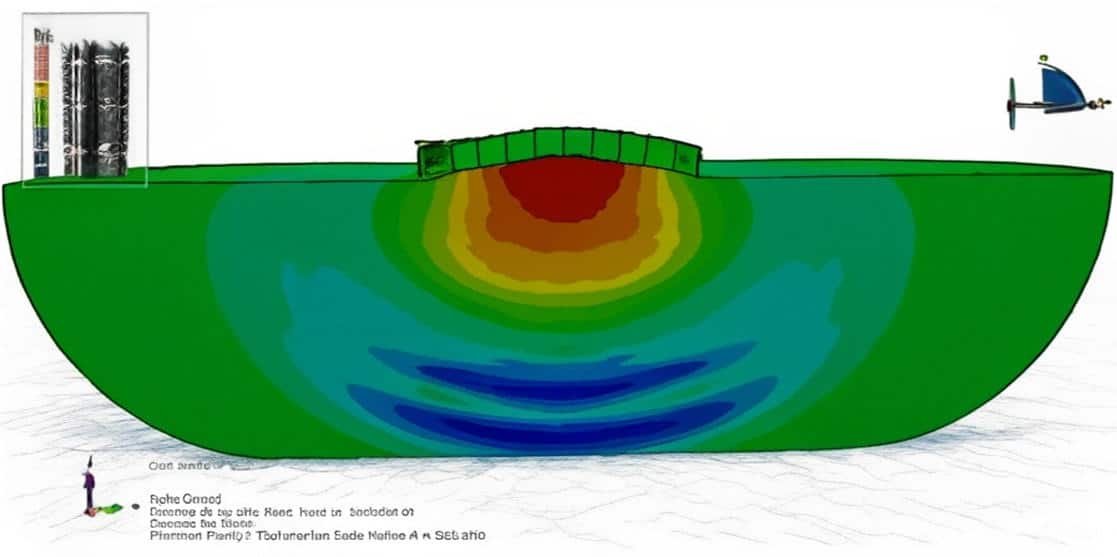
When an explosive detonates underwater, the rapid release of chemical energy generates a shock wave followed by bubble oscillations due to the expansion and contraction of detonation gases. These phenomena exert transient and oscillatory loads on nearby structures such as ships, submarines, or underwater pipelines.
Underground Explosions (UGEX):
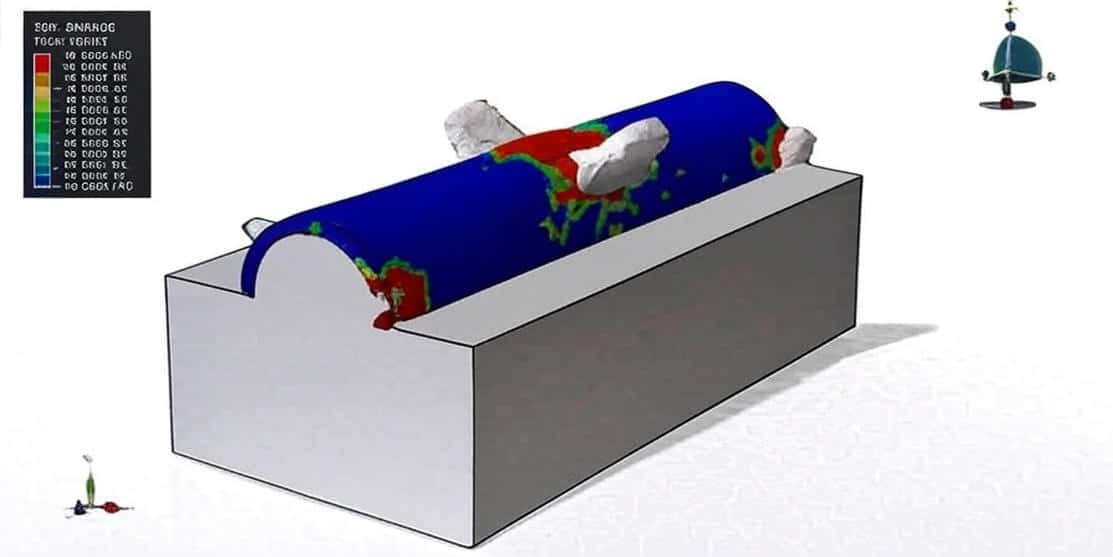
In soil or rock, the explosion produces a shock front that rapidly transitions into a stress wave as it travels through heterogeneous geological materials. The resulting wave propagation, reflection, and attenuation influence crater formation, ground motion, and structural damage in nearby facilities or tunnels.

3. Simulation Objectives

Numerical simulations of these explosions aim to:

Predict pressure-time histories, impulse loads, and structural responses.
Analyze shock wave propagation, bubble dynamics, and ground/soil deformation.
Reduce the need for costly full-scale experiments and improve design safety and blast mitigation strategies.

4. Modeling and Computational Approaches

Simulation and analysis typically employ advanced computational methods, including:

Finite Element Method (FEM): For solid structures and soil deformation under blast loading.
Finite Volume Method (FVM) and Smoothed Particle Hydrodynamics (SPH): For fluid or coupled fluid–structure interaction modeling.
Coupled Eulerian–Lagrangian (CEL) or Arbitrary Lagrangian–Eulerian (ALE) formulations: To model interactions between fluids (water/air) and solids (structures or ground).
Equation of State (EOS) models: Such as Jones–Wilkins–Lee (JWL) or Mie–Grüneisen, used to represent the thermodynamic behavior of explosives and surrounding media.

5. Key Analysis Aspects

Shock Wave Propagation: Understanding attenuation, reflection, and refraction in dense media.
Bubble Dynamics (for UNDEX): Studying oscillation cycles and their secondary loading effects.
Soil and Rock Response (for UGEX): Evaluating plastic deformation, compaction, and crack propagation.
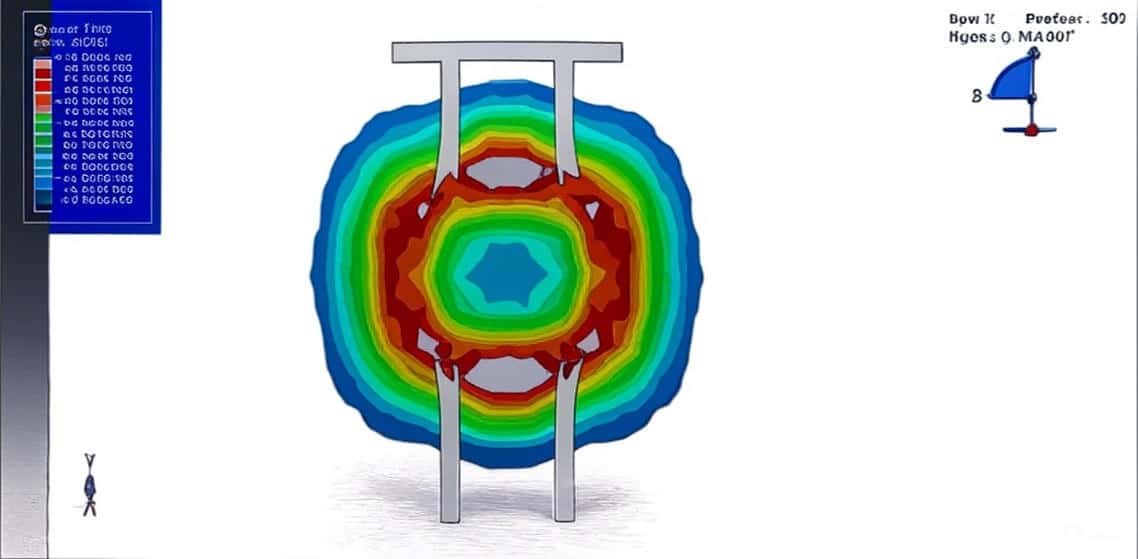
Structural Interaction: Assessing fluid–structure coupling effects and evaluating potential damage or failure mechanisms.

6. Applications

Naval Engineering: Hull design against underwater blasts.
Mining and Tunneling: Controlled underground detonations.
Civil Defense and Infrastructure: Blast-resistant design of tunnels, bunkers, and critical facilities.
Environmental Impact Studies: Assessing seismic or acoustic effects of underwater detonations.

7. Conclusion

Accurate simulation and analysis of underwater and underground explosions require multidisciplinary approaches combining computational mechanics, fluid dynamics, material science, and blast physics. With advancements in numerical solvers, high-performance computing, and experimental validation, engineers can now achieve reliable predictions of explosion effects and optimize protective or operational designs accordingly.

Course Content

Example-1: Numerical investigation of the damage characteristics of an ice sheet subjected to an underwater explosion
In this lesson, the numerical investigation of the damage characteristics of an ice sheet subjected to an underwater explosion is presented. The ice is modeled as a three-dimensional solid part, while the air, soil, water, and TNT are modeled as Eulerian parts. Ice jams are a common phenomenon in cold regions and tend to form easily, especially in rivers, lakes, and oceans above 30 degrees latitude during periods of freezing and thawing. However, ice jams can pose serious threats to human life and property. Therefore, developing more effective methods for preventing ice jams is essential. Some experts have suggested that using underwater explosions to break ice is an effective approach to eliminating ice jams. At present, underwater explosion ice-breaking is a complex fluid–structure interaction problem, and the mechanism of interaction between the fluid and ice has not yet been fully understood. To analyze this problem, three primary methods are commonly used: Theoretical analysis: A theoretical model is usually proposed based on certain assumptions. This method is suitable for simplified situations under idealized shock wave loads but is limited in handling complex problems. Experimental method: Experimental tests can be conducted under controlled parameter conditions to study the ice-breaking process; however, such tests are often expensive and time-consuming. Numerical method: By incorporating appropriate material models and failure criteria, computational techniques such as the finite element method can be employed to study the dynamic behavior of ice and the mechanisms of fluid–ice interaction. An underwater explosion is a complex fluid–solid coupling process involving medium flow, large structural deformation, and nonlinear failure. With the development of numerical methods, many researchers have improved computational techniques to enhance efficiency, such as modified Lagrangian methods, the Arbitrary Lagrangian–Eulerian (ALE) method, the Coupled Eulerian–Lagrangian (CEL) method, the Boundary Element Method (BEM), and Smoothed Particle Hydrodynamics (SPH). Each method has its own advantages and limitations. Due to their high computational efficiency and ability to handle complex models, both the ALE and CEL methods have been successfully implemented in commercial software and are widely used for solving various engineering problems, particularly underwater explosion analyses. However, although the CEL method effectively combines Eulerian and Lagrangian formulations—where fluid motion is described by the Eulerian approach and structures by the Lagrangian approach—there is still a lack of comprehensive material models for ice in ABAQUS/Explicit.

Abaqus Files
Document
Tutorial Video-1

30:58
Tutorial Video-2

00:34

Example-2: Analysis of the concrete-filled double skin steel tubular (CFDST) structure subjected to an underwater explosion
In this section, the analysis of a concrete-filled double-skin steel tubular (CFDST) structure subjected to an underwater explosion is presented. The concrete column is modeled as a three-dimensional solid part, while the inner and outer steel tubes are modeled as shell parts. The air, water, and TNT are represented as three-dimensional Eulerian parts. Underwater explosions (UNDEX) have become one of the primary threats to the safety of marine and offshore structures. Therefore, improving the underwater blast resistance of such structures has become an essential defensive and anti-terrorism measure worldwide. It is increasingly important to investigate the structural behavior of components subjected to UNDEX loading. The methodologies used for UNDEX investigations include experimental testing and numerical modeling. Compared with field tests—which are generally time-consuming and costly—finite element analysis (FEA) is often preferred due to its high efficiency and ability to handle a comprehensive range of parameters. Hence, the present study adopts the FEA method to investigate the UNDEX response of structures. A concrete-filled double-skin steel tube (CFDST) consists of an inner steel tube and an outer steel tube, with concrete filled in the annular space between them. CFDSTs are increasingly being used in offshore structures, such as submarine pipelines, due to their high strength, ductility, and energy absorption capacity. To model the concrete behavior under severe loading, the Concrete Damaged Plasticity (CDP) model with strain damage capability is employed. The Johnson–Cook damage and hardening models are used for the steel tubes to account for high-strain-rate effects. The Jones–Wilkins–Lee (JWL) equation of state (EOS) is adopted to define the TNT explosive material, while the Us–Up relationship is used for water, and the ideal gas EOS is applied for air. A dynamic explicit step is used to analyze the underwater explosion event. All contacts in the domain are defined using appropriate contact properties, and suitable mechanical and Eulerian boundary conditions are applied to the respective parts.

Example-3: Underwater explosion simulation using the CEL method near a floating structure
In this case, the underwater explosion simulation using the CEL method near a floating structure is studied. The aluminum hull is modeled as a three-dimensional thick shell part. The Soil, TNT, Water, and Air are modeled as three-dimensional parts inside the Eulerian domain. Underwater explosion involves many difficult problems, such as problems of fluid–solid coupling and additional water mass and liquid jets. In most cases, damage done to structures occurs early on and is due to the striking of the shock wave. All ships are liable to collisions, and in wartime, they are liable to enemy attack. The most serious threats to a ship’s survival are probably collision or an underwater explosion. Collisions are dealt with under damage stability. The detonation of an explosive device leads to the creation of a pulsating bubble of gas containing about half the energy of the explosion. The field of underwater explosions and shock physics is both complex and fascinating. Many aspects of the underwater explosion event must be studied properly to understand the development and propagation of the dynamic shock loading through the fluid. To model TNT or explosive material, the JWL equation of state is selected. The JWL equation of state (EOS) is frequently used for the products (and sometimes reactants) of a high explosive (HE). Here, we review and systematically derive important properties. The JWL EOS is of the Mie-Grueneisen form with a constant Grueneisen coefficient and a constant specific heat. To model soil behavior, the More-Coulomb plasticity with elastic data is selected. To model water, the Us-Up linear shock model is considered. The Air is modeled as an ideal gas. To model aluminum behavior under severe load, the Johnson-Cook hardening and damage model is selected The dynamic explicit step with a general contact capability is used in this tutorial; the general contact algorithm is suitable here because of the complex contact situation. The proper mechanical and Eulerian boundaries are assigned to the parts. The uniform material method to define the mass and volume of the TNT and other parts is considered.

Example-4: Underwater explosion shock on a cylindrical aluminum shell in interaction with soil
In this lesson, the underwater explosion shock on a cylindrical aluminum shell in interaction with soil is investigated. The water is modeled as a three-dimensional solid part with acoustic behaviour. The aluminum part is modeled as a three-dimensional shell part, and the soil as a solid part. In modern warfare, the role of naval warfare is becoming increasingly critical. Since World War II, scholars have been conducting systematic research on UNDEX.In particular, the underwater precision strike in war bears a complex nature and often occurs in a non-contact explosion in the vicinity of the target. The damaging impact of a blast is related to the explosion source and is closely related to the stand-off distance, surrounding medium, target size, material properties, and other factors. In the case of near-field explosions, the target is influenced by the initiation process, detonation products, shock waves, etc. The distance from the detonation center progressively weakens the impact of detonation products on the target and shock wave energy. However, for far-field explosions, the initiation of the explosion is not the focus of this study, and comparatively, the process of shock wave propagation and the effect of damage are more crucial. The persistence of shock waves is related to the surrounding medium in the propagation process. The shock wave generated by the explosion is fundamentally related to the transmission of the response state of the medium To model water behaviour, the acoustic medium property is selected. To model aluminum behaviour, the elastic-plastic model with the Johnson-Cook damage criterion is considered. The soil is modeled as an elastic material with Mohr-Coulomb plasticity. The dynamic explicit step is appropriate for this type of analysis. The perfect contact is assumed between the water and the oil, the water and the shell part. The UNDEX method, as the incident wave model, is selected to transfer the pressure load through the water.

Example-5: Underwater explosion near a concrete dam using the CEL method
In this section, the underwater explosion near a concrete dam using the CEL method is presented. The dam is modeled as a three-dimensional part. The TNT, water, and air are modeled as the Eulerian part. An underwater explosion (UNDEX) occurs when an explosive detonates beneath the water surface, releasing a large amount of energy in a very short time. This rapid energy release generates a high-intensity shock wave, followed by the formation and oscillation of a gas bubble. These dynamic effects can cause severe pressure loading and structural damage to nearby marine or offshore structures, such as ships, submarines, and underwater pipelines. Underwater explosion analysis aims to understand and predict the interaction between the explosion-induced shock waves, the surrounding fluid, and the affected structures. Because direct experimental testing is costly and complex, numerical simulation techniques—such as the Finite Element Method (FEM), Arbitrary Lagrangian–Eulerian (ALE), and Coupled Eulerian–Lagrangian (CEL) methods—are widely used to model these events. These methods help capture the complex fluid–structure interaction (FSI) phenomena and provide insights into pressure distribution, structural response, and potential failure mechanisms. To model air behavior, an ideal gas formulation with viscosity is used. Water is modeled as the Us-Up equation of state, TNT is modeled as the JWL equation to convert chemical energy release from the explosion process to mechanical pressure. To model concrete behavior, Abaqus gives some material models like CDP and Brittle, which are not suitable to model progressive damage under a detonation pulse. The dynamic explicit step with general contact as interaction is used. To model the Eulerian material, there are two ways: Volume fraction and uniform material. In this tutorial, uniform material is used to specify the water, the TNT, and the air amount and location. At the first of the analysis, each material has to fix its location, but during the simulation, the volume of the Eulerian parts mixes.

Example-6: Analysis of the RC slab subjected to an underwater explosion using the CEL method
In this case, the analysis of the RC slab subjected to an underwater explosion using the CEL method is presented. The Eulerian part contains TNT, air, and water is modeled as a three-dimensional Eulerian part. The concrete slab is modeled as a three-dimensional solid part. The steel reinforcement is modeled as a three-dimensional wire part. The prediction of damage and failure of structures subjected to underwater explosions (UNDEX) is of particular importance to marine applications. The dynamic response of structures in the vicinity of UNDEX is complicated, involving detonations of explosives, propagation of shock waves, pulsations of gas bubbles, fluid-structure interaction, nonlinear vibration of structures, and so on. The explosive charges can be modeled by the Jones-Wilkins-Lee equation of state, which converts chemical energy released from the explosion to the mechanical pressure. For the water, the Us-Up equation of state is selected. To define air, the equation of state for an ideal gas type is considered. To model steel reinforcement under severe loads like explosion shock, an elastic-plastic model with ductile damage criterion is used. The Abaqus has some material models to define concrete behavior under blast load and during the explosion, huge damage will be created on the slab surfaces, so the proper material model must be selected, and it can be defined as a code and modified in the input file. The dynamic explicit step and general contact algorithm are appropriate for this type of analysis. The embedded constraint is assigned to the reinforcement as an embedded region inside the concrete host. The fixed boundary condition is assigned to the bottom surface and side surfaces of the slab. To model Eulerian material, the volume fraction method and uniform material can be implied.

Example-7: Underwater explosion based on the Eulerian finite element approach
In this lesson, the underwater explosion based on the Eulerian finite element approach is studied. The main phenomena of underwater explosions include shock wave formation and propagation, bubble pulsation, and migration. Generally, considering the differences of time sequence and time scale, the process of underwater explosion is usually divided into two stages, i.e., the shock wave stage and bubble pulsation stage, and studied individually. At the former stage, the duration of the shock wave is in milliseconds, and the peak pressure can be up to the level of GPa.This stage is usually featured by strong nonlinearity, and the compressibility of the fluid should be considered. In this tutorial, all parts are modeled as three-dimensional Eulerian parts. TNT behavior is modeled as JWL material, which can convert chemical energy release from the explosion process to mechanical pressure; water is modeled as the Us-Up equation of state, and air is modeled as an ideal gas. A dynamic explicit step is appropriate for this type of analysis, and proper boundary conditions are assigned to the part. To use the Eulerian procedure, it is necessary to use the volume fraction method or the uniform material method to locate the Eulerian material. In this tutorial uniform material procedure is used. The mesh quality has a huge effect on the wave propagation, so using a small mesh is necessary. After the simulation, the wave propagation inside the water and air is clear

Example-8: Analysis of the craters produced by an underground explosion using the Eulerian method
In this section, the analysis of the craters produced by an underground explosion using the Eulerian method is investigated. Tests of crater formation are appropriate tools to study the blast phenomena, the behavior and destructive power of different explosives, and the response of soils and rocks under this type of load. The mechanism of crater formation is complex, and it is related to the dynamic physical properties of air, soil, and the air/soil interface. Even very carefully performed cratering tests give deviations in the dimensions measured of about 10%, while differences of as much as 30–40% % are common. A cavity is always formed when a confined explosion is produced in a mass of soil. If the explosion is close to the surface, a crater is formed, and a complex interaction takes place between gravity effects, soil strength, and transient load conditions. The most important variables in defining the crater shape and size are the mass W of the explosive and the depth of the detonation beneath the air/soil interface. When d 0 when the explosive is detonated beneath the soil surface. For Ford> 0, the crater mechanism is altered by gravitational effects. When the depth of the detonation increases, larger amounts of subsoil must be expelled by the explosion. Thus, the crater radius and the depth of the crater increase when d increases, until a certain limit value, from which they rapidly decrease. To model air behavior, EOS(Equation of State) as an ideal gas with viscosity, to model soil elasticity with Mohr-Coulomb plasticity, and the JWL equation has been implied for TNT. A dynamic explicit procedure is appropriate for this type of analysis. During the explosion, the TNT wave as a pressure load created a huge crater inside the soil.

Example-9: Numerical analysis of the failure modes of concrete gravity dams subjected to underwater explosion
In this case, the numerical analysis of the failure modes of concrete gravity dams subjected to underwater explosion is presented. With the increased world tension, terrorist bombing attacks or accidental explosions are becoming a large threat to infrastructure such as important economic, military, and civilian facilities. The research on the anti-knock safety of structures has increasingly attracted people’s attention. In order to meet the ever-increasing demand for power, irrigation, and drinking water, the majority of high dams are being built or to be built. Considering their significant political and economic benefits, undoubtedly, high dams might be targeted by terrorists because the possible failure of dams can cause economic disaster, a large number of casualties, and garner significant media attention. Since the September 11 attacks by terrorists, there has been increasing public concern about the threat of bomb attacks on dam structures. Therefore, protection of dam structures against blast loads is an important component of homeland security. Study on the failure modes and antiknock performance of concrete gravity dams subjected to underwater explosion is crucial to evaluate their antiknock safety. While, the physical processes during an explosive detonated in water and shock wave propagation are extremely complex, and the subsequent response of the dam subjected to explosion shock loading is much more complicated than that under other loadings such as static and earthquake loadings To define the correct behavior for concrete under high strain rate and huge stress, it is necessary to use an appropriate material model to consider damage . A dynamic explicit step with the UNDEX procedure has been used During the process, the damage distribution is obvious and the damage can be changed by increasing or decreasing the amount of TNT or changing the position of the source point as the TNT source.

Example-10: Coupled acoustic–structural response analysis of a hull subject to underwater explosion
In this lesson, the coupled acoustic–structural response analysis of a hull subject to underwater explosion is studied. The coupled acoustic–structural response analysis of a hull subject to an underwater explosion (UNDEX) examines how the structure (the hull) and the surrounding fluid (water) interact dynamically when exposed to a blast. In such events, the underwater explosion generates a shock wave that travels rapidly through the water and impinges on the hull surface. This causes pressure loading on the structure, inducing vibrations, deformations, and potential damage. Because the water and the hull influence each other’s responses—pressure waves in the fluid affect the structure’s motion, and the structure’s motion, in turn, radiates waves back into the water—the problem must be treated as a fully coupled acoustic–structural system. Non-contact underwater explosion is the major source of threat to ships and submarines. Thus, non-contact underwater explosion to the responses and damages of submerged structures is divided into two categories: near-field explosion and far-field explosion. Dynamic explicit analysis is appropriate for this type of simulation.

Example-11: Underwater explosion using the acoustic method near a circular plate-Paper verification
In this section, the underwater explosion using the acoustic method near a circular plate is investigated. Far-Field UNDEX models must typically treat two UNDEX phenomena: shock loading and cavitation. Shock loading occurs as a result of the incident explosive shock wave impinging on the wet surface of the ship structure. Cavitation occurs because the pressure in the surrounding water drops below its vapor pressure due to the tensile wave reflected from the ship(local cavitation) or from the free surface (bulk cavitation). The most common numerical method used to model far-field UNDEX is the finite element method (FEM). Considering shock loading and cavitation in FEM models creates inherent difficulties in creating an accurate model. Shock waves are characterized by a discontinuous rise in pressure followed by a brief period of exponential decay. Discontinuities can not be captured exactly in a FEM scheme; thus, in the far-field problem, distortion of the wave front and loss of pressure magnitude are two difficulties that must be overcome when modeling the explosive shock wave. Cavitation is a non-linear phenomenon that requires specific treatment in the governing equations of the far-field model. Abaqus explicit is appropriate for this type of analysis. During the analysis, pressure from the TNT charge causes large deformation inside the plate.

Example-12: Analysis of a stiffened panel subjected to underwater shock
In this case, the analysis of a stiffened panel subjected to underwater shock is presented. The analysis of a stiffened panel subjected to an underwater shock is an essential aspect of naval and marine structural design, particularly for warships, submarines, and other underwater vehicles. When an underwater explosion (UNDEX) occurs near a hull or structural component, a high-intensity pressure wave propagates through the water and impinges upon the structure. This results in a complex, transient interaction between the fluid medium and the structural system. A stiffened panel, representing a segment of a ship’s hull or bulkhead, typically consists of a thin plate reinforced by longitudinal and transverse stiffeners. Under shock loading, the dynamic response of this panel involves local plate deformation, stiffener bending, membrane stretching, and global vibration modes. The interaction between the fluid pressure and structural motion—commonly modeled through coupled acoustic–structural formulations—governs the transient behavior and potential for damage or failure. Accurate analysis of this phenomenon requires consideration of several factors: the characteristics of the shock wave (peak pressure, duration, decay), the fluid–structure coupling, geometric and material nonlinearities, and potential structural damping. Numerical methods such as finite element (FE) and boundary element (BE) techniques are widely used to simulate the response, often validated against experimental or empirical data. Understanding the dynamic behavior of stiffened panels under underwater shock loading is crucial for improving hull resilience, optimizing structural design, and enhancing the overall survivability of marine structures in explosive environments.

Example-13: Underwater explosion (UNDEX) analysis using the Eulerian method
Underwater explosions (UNDEX) produce highly transient, high-pressure shock waves that propagate through the surrounding fluid medium and can cause severe loading on nearby marine or naval structures. Accurate modeling of this phenomenon is essential for assessing structural integrity, hull survivability, and overall ship safety. Because of the complex nature of fluid dynamics and fluid–structure interaction involved, computational methods play a central role in UNDEX analysis. The Eulerian method is widely used to model the fluid domain in underwater explosion simulations. In this formulation, the computational mesh is fixed in space, and the fluid (usually water and explosive gas products) moves through the mesh. This approach allows for the accurate capture of large deformations, free-surface motion, and shock wave propagation without the mesh distortion issues commonly encountered in purely Lagrangian descriptions. In UNDEX analysis, the explosive detonation and subsequent shock wave propagation are modeled within an Eulerian fluid domain, often coupled with a Lagrangian structural domain (in a so-called coupled Eulerian–Lagrangian or CEL framework). This coupling enables the realistic simulation of fluid–structure interaction (FSI), where the shock wave impinges upon and reflects from a deformable structure such as a ship hull or stiffened panel. The Eulerian method provides several advantages: it can accurately capture the shock front, model cavitation effects, and represent complex interactions between different media (water, air, and detonation gases). However, it also demands significant computational resources and careful numerical treatment to ensure stability and precision in pressure wave resolution. In this lesson, the underwater explosion (UNDEX) analysis using the Eulerian method is studied. Overall, the Eulerian approach is a powerful tool for understanding and predicting the physical phenomena associated with underwater explosions, offering valuable insights for designing more resilient naval and marine structures. TNT and water have been modeled as Eulerian parts, and the Structure as a Lagrangian part. For modeling TNT behavior JWL equation of state and for the water, Us-Up has been used. For predicting damage in the structure, an appropriate model has been used. During the analysis structure failed, and TNT pressure destroyed the structure

Example-14: Shock response analysis of a marine sandwich structure subjected to UNDEX loading
In this section, the shock response analysis of a marine sandwich structure subjected to UNDEX loading is investigated. In modern sea combat, in which strike power has increased markedly, the structures of naval ships must be designed to withstand shock loads resulting from weapon hits. To improve the design of naval ships such that they can withstand air blasts or underwater shock loads, one must determine the structural damage to naval ships from shock loads. When an explosive is detonated in water, the sudden release of chemical energy generates a high-pressure gas that markedly exceeds hydrostatic pressure. An explosion, therefore, generates shock waves and gas bubbles. Since the explosion pressure exceeds the air shock wave, and the action time of the resulting underwater shock wave is shorter than the action time of the air shock wave, analyzing underwater explosions is complex and difficult. Steel material with elastic plastic behavior, coupled with damage for the sandwich structure and acoustic medium property for water, is used. A dynamic explicit procedure is appropriate for this type of analysis. The contact between the structure and water is considered a perfect contact. The UNDEX (Under Water Explosion) procedure is used to demonstrate the explosion phenomenon. The acoustic interaction is also assigned to the water. The sandwich structure and water are modeled as a three-dimensional part.

Example-15: Modeling of the CEL explosion in the depth of soil near the concrete piled raft structure
In this case, the modeling of the CEL explosion in the depth of soil near the concrete piled-raft structure is presented. The domain is modeled as a three-dimensional Eulerian part. The concrete piled raft is modeled as a three-dimensional solid part. The air, TNT, and soil are modeled as three-dimensional solid parts. An explosion may be initiated by various methods. However, the initiation of an explosion always goes through a stage in which a shock wave is an important feature. Jones–Wilkins (Lee or JWL material model is used to model the TNT behavior during the explosion. The Jones-Wilkins-Lee (or JWL) equation of state models the pressure generated by the release of chemical energy in an explosive. This model is implemented in a form referred to as a programmed burn, which means that the reaction and initiation of the explosive is not determined by shock in the material. Instead, the initiation time is determined by a geometric construction using the detonation wave speed and the distance of the material point from the detonation points. To model arri behavior, the ideal gas model as an equation of state is selected. To model soil, the Mohr-Coulomb plasticity is considered. The concrete material model should be specific because of the damage and failure that happens during the explosion. Abaqus has some material models that are available by using code. The dynamic explicit step is appropriate for this type of analysis. The general contact algorithm with the contact property is selected. All boundary conditions are assigned to the domain and concrete structure. To model Eulerian material, the volume fraction method is considered.

Example-16: ٍAnalysis of the hollow steel piles subjected to buried blast loading
In this lesson, the analysis of the hollow steel piles subjected to buried blast loading is studied. A pile is a load-bearing component of a structure that transfers the structural load to the hard soil or rock underground. The modern human civilization and smart infrastructure depend largely on the pile foundation for carrying its structural load because the pile foundation reduces the area of load distribution in the surroundings near the ground surface and thus, is considered a suitable foundation system in regions with more congestion and a higher number of tall buildings. However, failure of a single pile can lead to disaster by causing progressive failure of the superstructure and the surrounding structures. In recent decades, terrorist attacks and bomb blasts have caused the failure of several structures. A small magnitude of the blast, if it happens in the close vicinity of one pile, may lead to progressive failure of the whole structure. Moreover, the failure of the structure often starts from the soil because the soil is the weakest of all civil engineering materials. Hence, it is extremely necessary to understand the response of pile foundations in the soil when subjected to blast loading. In this simulation, piles are modeled as a three-dimensional part with elastic plastic material coupled with damage data, soil is modeled as a three-dimensional part with an Eulerian approach with elastic plastic behavior, and TNT is modeled as a sphere using by JWL material method. A dynamic explicit step with general contact is appropriate for this type of analysis.

Example-17: Blast response and failure analysis of the pile foundation subjected to the surface explosion
In this section, the blast response and failure analysis of the pile foundation subjected to the surface explosion are investigated. This tutorial presents the response of pile foundations to ground shocks induced by surface explosions using fully coupled and non-linear dynamic computer simulation techniques. A significant increase in terrorist attacks against significant and iconic buildings and other infrastructure components highlights the need for the blast-resistant design of the structures. Blast loads are short-duration dynamic loads, and their duration is very much shorter (about 1000 times) than that of earthquakes. Thus, structural response under blast loading could be significantly different from that under a loading with a much longer duration, such as an earthquake. An explosion on the ground surface generates both air-blast pressure and ground shock on structures that are close to the detonation point. However, wave propagation velocities are different for geo-materials and air, and as a consequence, the ground shock excites the structure foundation earlier than the air blast pressure arrives at the structure. The explosive charge was modeled using the high explosive burn material model and the Jones–Wilkin–Lee (JWL) equation of state (EOS). The air is modeled as an ideal gas, the soil with elastic plastic material, and for the pile, Johnson-Holmquist has been used.

Example-18: Modeling of the CEL explosion in the depth of soil near a solid steel pipe
In this case, the modeling of the CEL explosion in the depth of soil near a solid steel pipe is presented. The Eulerian domain is modeled as a three-dimensional Eulerian part. The air, soil, and TNT are modeled as a three-dimensional solid part. The steel pipe is modeled as a three-dimensional solid part. Buried pipelines are considered among the most important elements of lifelines. Buried pressurized gas pipelines are bound to be threatened by accidental explosions in process industries, explosives factories, open pit mines, quarries, public works, or even intentional explosions near a pipeline. Terrorist attacks have unfortunately been increasing so that multiple explosions, in recent years, have taken place along the route of oil and gas transmission pipelines. Accordingly, blast loads and the design and analysis of buried structures under destructive dynamic loads have received particular attention in recent years. To model steel pipe behavior under severe load, elastic-plastic material data is selected. The Johnson-Cook plasticity with Johnson-Cook damage to consider steel pipe failure during the detonation is used. To model air material, the ideal gas equation of state with dynamic viscosity is considered. To model soil behavior, elastic data with Mohr-Coulomb plasticity is used. The Jones-Wilkens-Lee (or JWL) equation of state models the pressure generated by the release of chemical energy in an explosive. This model is implemented in a form referred to as a programmed burn, which means that the reaction and initiation of the explosive is not determined by shock in the material. Instead, the initiation time is determined by a geometric construction using the detonation wave speed and the distance of the material point from the detonation points. The dynamic explicit step is appropriate for this type of analysis. The general contact capability with the contact property is used. The non-reflecting boundary is assigned to the outer surfaces of the Eulerian domain. The fixed boundary condition is assigned to the two ends of the pipe. The volume fraction method is used to define the location of each material in the Eulerian domain.

Example-19: Analysis of the tunnel in soil subjected to internal blast loading
In this lesson, the analysis of a tunnel in soil subjected to internal blast loading is presented. The concrete tunnel is modeled as a solid part, the surrounding domain as an Eulerian part, TNT and soil as solid materials, and the beam as a wire part. Underground roadway and railway tunnels, as well as tunnels for utility lines and water pipelines, are integral components of modern civil infrastructure. In recent decades, explosion incidents caused by terrorist activities inside underground facilities have become a growing threat to human safety. An internal explosion in a tunnel is often more hazardous than an explosion above ground due to multiple reflections of the blast-induced shock wave on the tunnel walls, which cause channeling and amplification of the pressure wave. Therefore, to safeguard tunnels against explosion incidents, it is essential to design them to adequately withstand blast loading. For this purpose, it is necessary to understand the response of tunnels subjected to blast loading, both experimentally and numerically. The present work focuses on the advanced numerical analysis of tunnels subjected to internal blast loading. In the model, steel beams are defined with elastic–plastic behavior coupled with a ductile damage criterion. The soil is modeled using an elastic–plastic material with a Mohr–Coulomb failure criterion. The TNT explosive is represented using the Jones–Wilkins–Lee (JWL) equation of state, while the concrete tunnel is modeled using the Johnson–Holmquist material model to account for high-pressure effects and failure. A dynamic explicit procedure is adopted, as it is suitable for this type of transient, high-rate analysis. General contact is defined for all contact interactions, and the embedded region technique is used to represent the beams within the concrete host. The Eulerian model employs the volume fraction method to define the location and amount of TNT. Appropriate boundary conditions are assigned to both the Eulerian domain and the concrete tunnel to ensure a realistic simulation of the blast event.

Example-20: Simulation of the CEL explosion in the stone tunnel in interaction with soil
In this section, the simulation of a coupled Eulerian–Lagrangian (CEL) explosion in a stone tunnel interacting with surrounding soil is investigated. The stone tunnel is modeled as a three-dimensional solid part, while the TNT and soil are represented as volumes within the Eulerian domain. The Jones–Wilkins–Lee (JWL) equation of state is used to model the behavior of the TNT explosive. This material model allows the conversion of the chemical energy released during detonation into mechanical pressure. Abaqus provides several material models for stone and rock, some of which are suitable for blast analysis, such as the Johnson–Holmquist (JH-2 or HJC) model. A dynamic explicit procedure is adopted, as it is appropriate for this type of transient, high-rate analysis. The general contact algorithm is used to model interactions among all parts with default contact properties. Fixed boundary conditions are applied to the bottom surfaces of the tunnel, and zero velocity conditions are assigned to the Eulerian domain boundaries. To represent the TNT and soil within the Eulerian domain, the volume fraction technique is used. This approach enables Abaqus to calculate the volume of solid materials within the Eulerian mesh. The mesh quality of both the tunnel and the Eulerian domain has a significant influence on the accuracy and stability of the simulation results.

Reviews

No Review Yet

28 people watching this product now!

Related Products

Deformation behavior of super-austenitic stainless steel sandwich panels subjected to air blast and underwater explosion

Abaqus

High-velocity impact simulation of Rubber-Toughened Poly Methyl Methacrylate (RT-PMMA) reinforced with CFRP

Abaqus

Analysis of the bolted steel splice connections under fire-Sequential Method

Abaqus

Static and dynamic compression test of a square cold-formed UHPC-filled dual steel stiffened slender column

Abaqus

Analysis of ceramic-UHMWPE armor penetration resistance against ballistic bullet impact

Abaqus

Analysis of the CEL sequential underwater explosion near a steel pipeline

Abaqus

Fire analysis of the CFRP composite material in Abaqus

Abaqus

Bond–Slip Analysis of the Pull-Out Test Simulation

Abaqus

Underwater and Underground Explosions Simulation and Analysis Package

Material Includes

Audience

What You Will Learn?

About Course

Introduction to Underwater and Underground Explosions: Simulation and Analysis

1. Overview

2. Nature of the Explosions

3. Simulation Objectives

4. Modeling and Computational Approaches

5. Key Analysis Aspects

6. Applications

7. Conclusion

Course Content

Abaqus Files

Document

Tutorial Video-1

Tutorial Video-2

Abaqus Files

Document

Tutorial Video

Abaqus Files

Tutorial Video

Abaqus Files

Document

Tutorial Video

Abaqus Files

Tutorial Video-1

Tutorial Video-2

Abaqus Files

Document

Tutorial Video-1

Tutorial Video-2

Abaqus Files

Document

Tutorial Video

Abaqus Files

Document

Tutorial Video

Abaqus Files

Tutorial Video-1

Tutorial Video-2

Abaqus Files

Document

Tutorial Video

Abaqus Files

Document

Tutorial Video

Abaqus Files

Document

Tutorial Video

Abaqus Files

Tutorial Video

Abaqus Files

Document

Tutorial Video

Abaqus Files

Document

Tutorial Video-1

Tutorial Video-2

Abaqus Files

Document

Tutorial Video

Abaqus Files

Document

Tutorial Video

Abaqus Files

Document

Tutorial Video

Abaqus Files

Document

Tutorial Video-1

Tutorial Video-2

Abaqus Files

Document

Tutorial Video-1

Tutorial Video-2

Reviews

Material Includes

Audience