

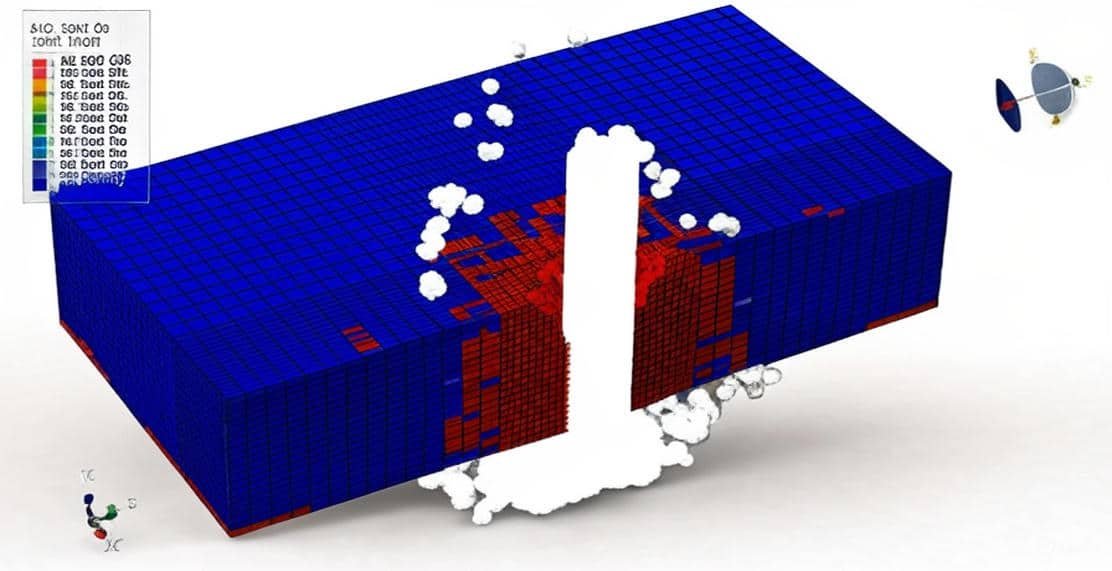
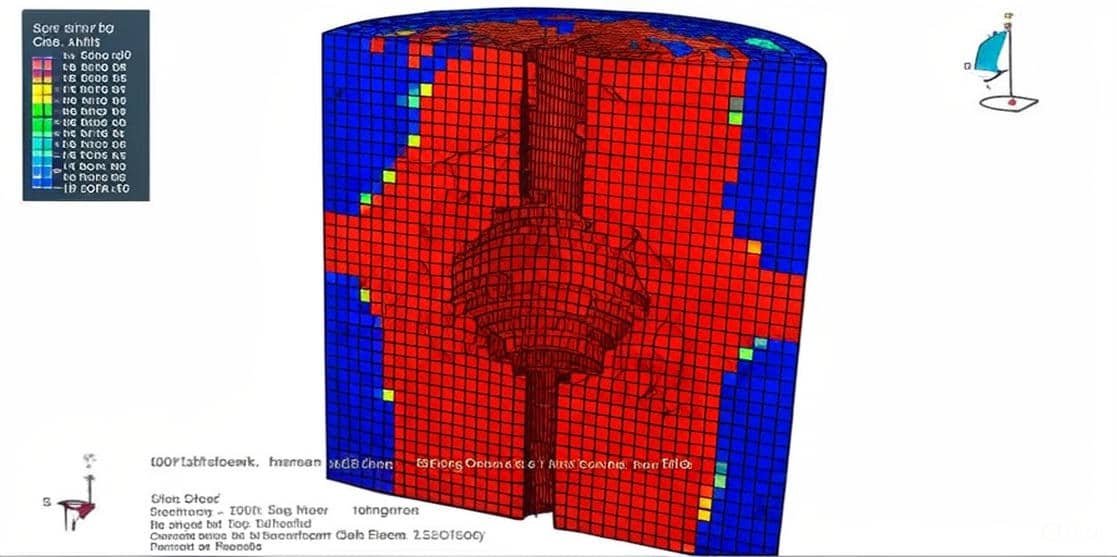
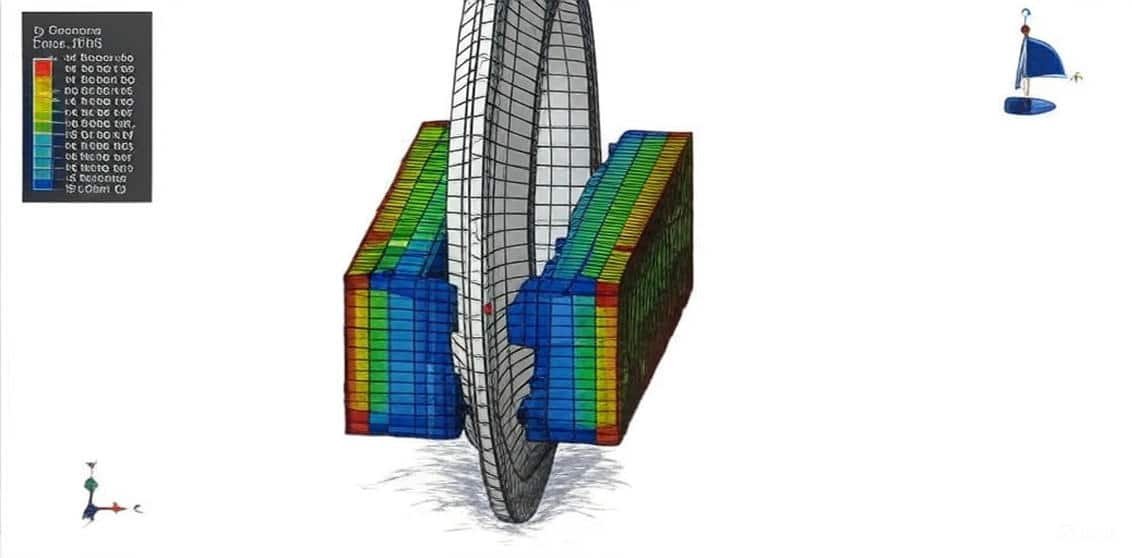
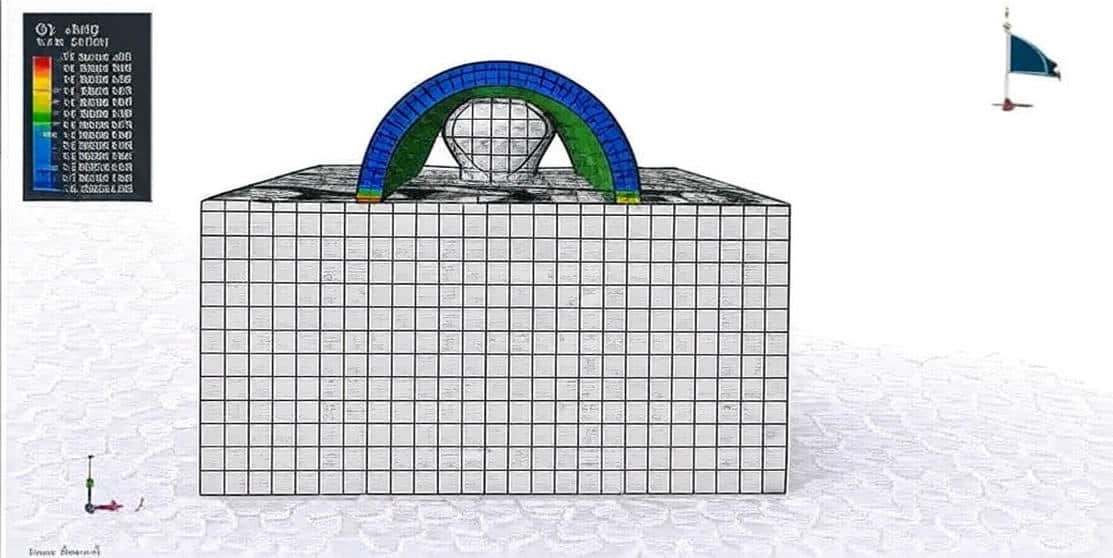
The mechanical behavior of rock and stone under dynamic loading conditions is a critical area of study in geotechnical, civil, and mining engineering. Natural and engineered rock masses are frequently subjected to dynamic forces arising from blasting, earthquakes, impact loads, machine vibrations, and excavation activities. Unlike static loading, dynamic effects introduce complexities such as stress wave propagation, rate-dependent material behavior, crack initiation, and progressive failure mechanisms. Understanding these responses is essential for ensuring the stability and safety of underground excavations, tunnels, slopes, and foundations.
In this package, through 10 comprehensive tutorials, all matters related to the rock and stone are explained in many simulations, such as explosion, impact, TBM cutting, foundation,…
The Finite Element Method (FEM) has emerged as a powerful numerical technique for investigating the dynamic response of rock and stone. FEM allows the discretization of complex geometries and heterogeneous materials into smaller elements, making it possible to capture stress distribution, displacement fields, and fracture evolution with high precision. Through dynamic analysis, FEM provides insights into time-dependent processes such as wave propagation, resonance phenomena, and energy dissipation mechanisms.
Dynamic FEM analysis of rock and stone typically involves modeling the material’s constitutive behavior, incorporating damping and inertia effects, and applying appropriate boundary conditions to simulate realistic field scenarios. Advanced formulations, such as explicit time integration and contact modeling, are often employed to accurately capture high-strain-rate deformations and fracture propagation. Moreover, FEM can be coupled with fracture mechanics, damage models, and discontinuum approaches to better represent the inherent heterogeneity and anisotropy of rock masses.
By leveraging FEM-based dynamic analysis, engineers and researchers can predict failure modes, optimize blasting designs, assess seismic stability, and develop safer infrastructure in rock engineering projects. As computational power and constitutive modeling techniques continue to advance, FEM remains a cornerstone for understanding and mitigating dynamic challenges in rock mechanics.

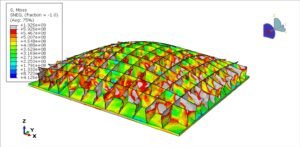
Abaqus
€68,00 €34,00
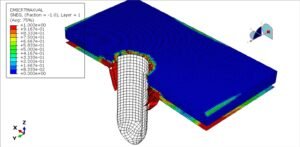
Abaqus
€77,00 €39,00
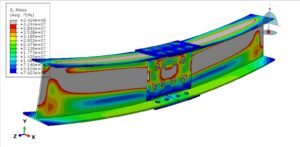
Abaqus
€79,00 €39,00
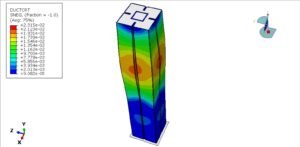
Abaqus
€75,00 €37,00

Abaqus
€76,00 €38,00
Abaqus
€79,00 €38,00
See more

Want to receive push notifications for all major on-site activities?