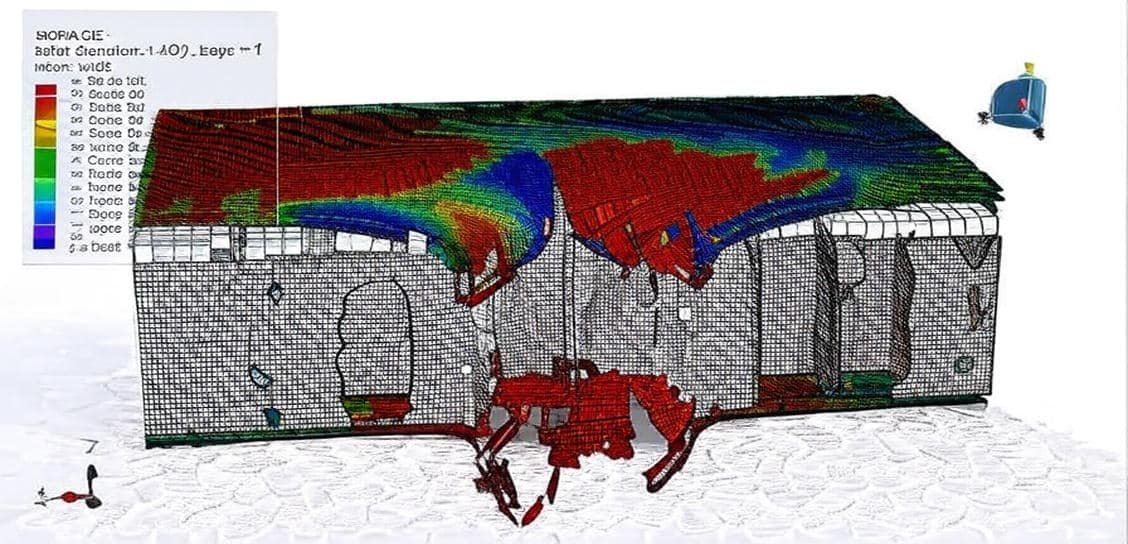
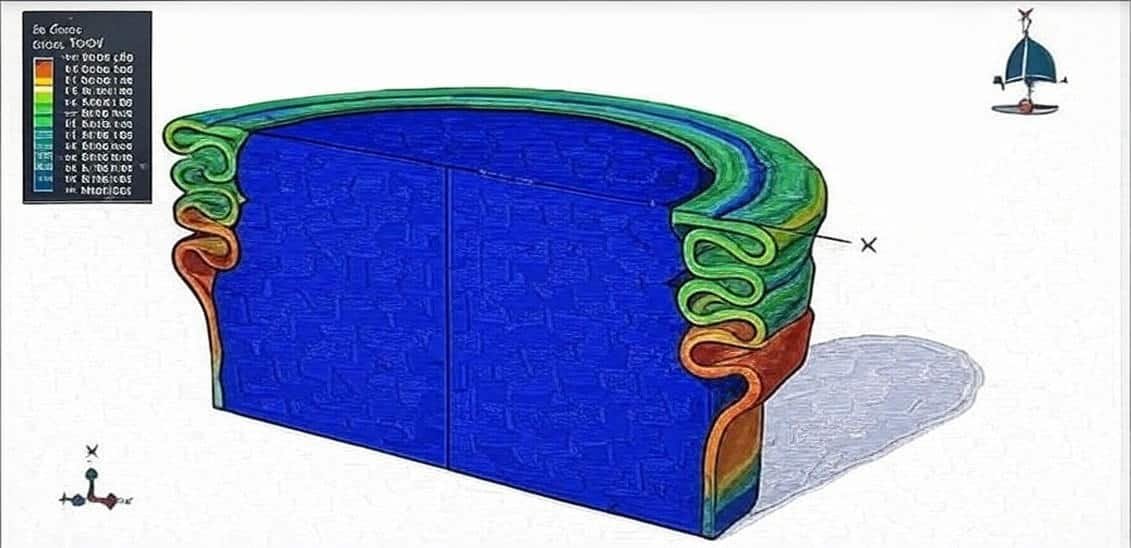
Polymer and Metal Foam Analysis Package in Abaqus

Categories: Abaqus, Course, Dynamic, Explosion, Finite Element, Impact Engineering

Polymer and Metal Foam Analysis Package in Abaqus

Peyman Karampour

Level

Intermediate
Duration

8 hours 50 minutes
Last Updated

September 4, 2025
Certificate

Certificate of completion

29 people watching this product now!

About Course

📘 Introduction to Polymer and Metal Foam Analysis

1. Metal and Polymer foam

Polymers
Polymers are long-chain molecules with diverse mechanical, thermal, and chemical properties. They are widely used in structural, biomedical, and automotive applications due to their light weight, flexibility, and tunable behavior (elastic, viscoelastic, or plastic).
Metal Foams
Metal foams are lightweight, porous structures created by introducing gas bubbles into molten metal. They combine high strength with low density, excellent energy absorption, and thermal/electrical conductivity. Common applications include crash protection, aerospace components, and thermal management systems.

This package includes 20 practical tutorials that cover all about polymer and metal foam.

2. Why Analyze Them Together?

The combination of polymers and metal foams leads to hybrid materials that exhibit a balance of toughness, light weight, and multifunctional performance. For example:

Polymer-metal foam composites can be used in impact-resistant panels.
Polymer infiltration of metal foams creates advanced structural materials with improved energy absorption.
Understanding their coupled mechanical, thermal, and failure behavior is essential for engineering design.

3. Key Analysis Challenges

Heterogeneous microstructure: Random foam cell distributions and polymer chain networks require specialized modeling.
Nonlinear material behavior: Both polymers (viscoelasticity, plasticity) and foams (crushing, densification) exhibit nonlinear stress-strain responses.
Coupled phenomena: Mechanical, thermal, and fatigue interactions must often be considered simultaneously.

4. Simulation in Abaqus

Abaqus provides a robust platform for simulating polymer and metal foam behavior through:

Material Models
- Hyperelastic & viscoelastic models for polymers.
- Crushable foam and porous metal plasticity models for foams.
Multiscale Modeling
- Micromechanical cell models (RVE – Representative Volume Element).
- Continuum models for large structures.
Failure and Damage Analysis
- Progressive collapse in foams.
- Crack propagation in polymer-foam composites.
Applications
- Impact/Crashworthiness simulations.
- Thermal insulation and heat transfer analysis.
- Lightweight structural component design.

5. Applications in Industry

Automotive: Crash absorbers, lightweight panels.
Aerospace: High-strength-to-weight ratio components.
Biomedical: Porous implants mimicking bone structure.
Energy: Heat exchangers, battery casings, and hydrogen storage.

✅ In summary:
Polymer and metal foam analysis is a critical research and engineering field that aims to understand and predict the complex behavior of these advanced materials. Using simulation tools like Abaqus, engineers can optimize design, reduce experimental costs, and accelerate innovation in lightweight and high-performance structures.

Course Content

Example-1: Analysis of the CFRP facings and PET foam core panel under air blast load
In this lesson, the analysis of the CFRP facings and PET foam core panel under air blast load in Abaqus is studied. The CFRP sheets are modeled as three-dimensional parts with sixteen layers, and the Polyethylene terephthalate(PET) foam is modeled as a three-dimensional solid part. To model CFRP failure under severe blast load, the elastic model and damage behavior are considered. The foam is modeled as an elastic with crushable foam modeled as plastic hardening. The dynamic explicit step is appropriate for this type of simulation. Proper interactions and boundaries are assigned to all parts. The CONWEP air blast load procedure is selected to define the explosion. The appropriate choice of material model, being suitable for the description of stress-strain relation in a foam, is important. However, various foams have extremely different properties; thus, the task is not so simple, and each type of foam needs to be carefully analyzed. Usually, experimental identification of the material properties of the foam is done. Procedures exist, according to ISO or ASTM standards, that enable the determination of the core’s elastic and strength properties, which are also valid for PET foams. Moreover, technical data sheets are provided for foams that are available on the market, which include information on the most important material properties declared by producers and identified according to the aforementioned standards. In such a case, it seems that the description of material behavior should be easier. Nevertheless, the standards give recommendations that can be helpful only when the elastic response of the core is considered. What is more, the fact that the foam can be generally anisotropic is not commented on. For these reasons, some difficulties can be encountered when detailed analyses of sandwich response are done, and identification of the foam core materials' properties according to standards seems to be insufficient in such a situation

Abaqus Files
Document
Tutorial Video

24:01

Example-2: Simulation of the RC slab with PET foam core under thefour-point bending test
In this section, the simulation of the RC slab with PET foam core under the four-point bending test in Abaqus is investigated. The concrete and PET foam are modeled as three-dimensional solid parts. The steel reinforcements are modeled as wire parts. The appropriate choice of material model, being suitable for the description of stress-strain relation in a foam, is important. However, various foams have extremely different properties; thus, the task is not so simple, and each type of foam needs to be carefully analyzed. Usually, experimental identification of the material properties of the foam is done. Procedures exist, according to for example ISO or ASTM standards, that enable the determination of elastic and strength properties of the core, which are valid for PET foams as well. What is more, technical data sheets are provided for foams that are available on the market, which include information on the most important material properties declared by producers and identified according to the aforementioned standards. In such a case, it seems that the description of material behavior should be easier. Nevertheless, the standards give recommendations that can be helpful only when the elastic response of the core is considered. What is more, the fact that the foam can be generally anisotropic is not commented on. For these reasons, some difficulties can be encountered when detailed analyses of sandwich response are done, and identification of the foam core materials' properties according to standards seems to be insufficient in such a situation.

Example-3: Foam-filled aluminum/CFRP hybrid tube against transverse impact
In this case, the foam-filled aluminum/CFRP hybrid tube against transverse impact in Abaqus software is done. The aluminum tube, CFRP, and aluminum foam are modeled as three-dimensional parts. The Johnson-Cook hardening and damage model are suitable to model aluminum behavior under rapid deformation. The Crushable foam model is selected for the metal foam core to consider large plastic deformation. Hashin’s damage criterion is considered the damage criterion of the CFRP composite material. Dynamic explicit steps with mass scale as the target time to reduce the time of the simulation, and neglecting the inertia effect are selected. Thin-walled structures made of conventional metals, such as aluminum alloy and high-strength steel, have been extensively used as energy-absorbing components in vehicles to ensure their structural crashworthiness for reducing casualties and protecting cargo in case of crash accidents. Thin-walled metallic structures are of significant advantages, such as ductile behaviors and stable plastic collapse, making them dissipate collision energy in a more controllable manner. However, with stringent transport safety regulations and heightened environmental requirements, it has become more and more challenging for conventional thin-walled metallic structures to enhance their performance further. As a compelling material, carbon fiber reinforced plastic (CFRP) composites are gaining growing interest in the modern automotive industry for their distinct advantages in lightweight and mechanical properties over conventional metallic counterparts. Despite the significant benefits, CFRP composites exhibit some noticeable drawbacks, such as higher material cost and unstable, brittle catastrophic failure mode, which, to a certain extent, restricts their extensive applications in the automotive industry.

Example-4: Analysis of the high-velocity impact on CFRP-Aluminum foam-Aluminum honeycomb-CFRP panel
In this lesson, the analysis of the high-velocity impact on CFRP-Aluminum foam-Aluminum honeycomb-CFRP panel is studied. The CFRP parts are modeled as three-dimensional parts with sixteen layers. The aluminum foam is modeled as a three-dimensional solid part. The aluminum honeycomb is modeled as a shell part. The Crushable foam and damage criterion are considered to model metal foam, like aluminum foam. The Johnson-Cook hardening and dynamic failure are used to model honeycomb behavior under severe load. The elastic and damage models are selected to define CFRP composite behavior. Fiber-reinforced composite sandwich structures have been increasingly used in many advanced engineering applications, from aircraft bodies, sports cars, ships, bridge decks, and piers, to beams and columns of buildings, due to their high specific strength, high stiffness, lightweight, and corrosion resistance. However, accumulated evidence shows their vulnerability when impacted by heavy objects, bird strikes, tool drops, and loadings due to collision incidents. Impact loads cause severe damage to sandwich structures internally and externally in terms of substantial reduction in the tensile, compressive, shear, and bending strength since the event is instantaneous and the corresponding load magnitude can be many times that of its static equivalent. Therefore, new strategies and designs to improve the impact resistance of such structures have been continually proposed and refined, rendering them an active research topic.

Example-5: Investigation of Rigid Impact on Steel Wire Reinforced Foam Core/Composite Skin Sandwich
In this section, the investigation of Rigid Impact on a Steel Wire-Reinforced Foam Core/Composite Skin Sandwich in Abaqus is conducted through a comprehensive tutorial. The rigid projectile is modeled as a three-dimensional shell part. The steel reinforcements are modeled as a wire part. The glass-epoxy part is modeled as a three-dimensional shell part with six layers. The metal foam is modeled as a three-dimensional solid part. For the steel reinforcement, the elastic-plastic model with damage criterion is considered. The JC model is so appropriate for the steel material under high-strain-rate load. The metal foam material is defined as an elastic property with Crushable foam damage to consider the compression and damage. An ABAQUS Dynamic/Explicit package is used for finite element modeling of low- and high-velocity impacts. An explicit method can solve the dynamic equation, and also consider element failure. The general contact algorithm with contact property is selected for this analysis.

Example-6: Analysis of the steel bullet impact on the armor panel(Ceramic- Aluminum Foam)
In this case, the analysis of the steel bullet impact on the armor panel(Ceramic- Aluminum Foam) is investigated. The ceramic and aluminum foams are modeled as three-dimensional solid parts. Because of the symmetry conditions, one-quarter of the whole model is selected to reduce the time of the simulation. Damage investigation is the aim of this simulation. To model steel bullet behavior, the elastic-plastic model with ductile and shear damage is used. Two main mechanisms can cause the fracture of a ductile metal: ductile fracture due to the nucleation, growth, and coalescence of voids; and shear fracture due to shear band localization. Based on phenomenological observations, these two mechanisms call for different forms of the criteria for the onset of damage. To model ceramic or silicon carbide material, the Johnson-Holmquist or JH2 model is selected. Ceramic materials are commonly used in armor protection applications. In recent years, Johnson, Holmquist, and their coworkers have developed a series of constitutive relations to simulate the response of ceramic materials under large strain, high strain rate, and high-pressure impacting conditions. The JH-2 model assumes that the damage variable increases progressively with plastic deformation. To model metal foam behavior, the crushable foam hardening and ductile damage criterion is used. A dynamic explicit step with general contact capability is appropriate for this type of analysis. The perfect contact is assumed between the ceramic and aluminum foam plates. The symmetry boundary conditions are assigned to the symmetry zones. The initial velocity is applied to the steel bullet as a predefined field. The mesh should be fine to obtain correct results.

Example-7: Simulation of the SPH explosion over the composite panel( Aluminum- Metal Foam)
In this lesson, the simulation of the SPH explosion over the composite panel( Aluminum- Metal Foam) in Abaqus is studied. The explosive part, or the TNT, is modeled as a three-dimensional solid part. The aluminum sheets are modeled as three-dimensional solid parts. The Aluminum Foam as a core is modeled as a three-dimensional solid part. To model TNT behavior the Jones-Wilkins-Lee equation of state is selected. The Jones-Wilkins-Lee (or JWL) equation of state models the pressure generated by the release of chemical energy in an explosive. This model is implemented in a form referred to as a programmed burn, which means that the reaction and initiation of the explosive are not determined by shock in the material. Instead, the initiation time is determined by a geometric construction using the detonation wave speed and the distance of the material point from the detonation points. To model aluminum behavior under severe load, the Johnson-Cook hardening and damage criterion is used. The aluminum foam is modeled as an elastic material with Crushable foam hardening. To consider damage and failure of the metal foam, the ductile damage criterion is selected. The dynamic explicit step is appropriate for this type of analysis. The perfect contact is assumed between the metal foam and the aluminum sheets.

Example-8: Analysis of the low-velocity impact on the CFRP-AL Foam-CFRP panel
In this case, the analysis of the low-velocity impact on the CFRP-AL Foam-CFRP panel is done through a practical tutorial. The CFRP is modeled as three-dimensional solid parts with four different fiber directions. The aluminum foam as a core part is modeled as a three-dimensional solid part. The projectile is modeled as a three-dimensional shell part. To model CFRP material, the elastic data with the failure stress parameter and also Hashin’s damage criterion are selected. To model metal foam behavior under impact load, the Crushable Foam model with hardening is used. The dynamic explicit step is appropriate for this type of analysis. The surface-to-surface contact with friction as a contact property is selected between the rigid projectile and the upper CFRP plate. The cohesive interaction by using stiffness parameters and also damage definition between CFRP sheets and foam core is used

Example-9: Blast resistance of the composite slab(ceramic-Aluminum foam) under sequential explosion
In this section, the blast resistance of the composite slab(ceramic-Aluminum foam) under sequential explosion is demonstrated through a comprehensive tutorial. The two ceramic layers are modeled as a three-dimensional solid part. The aluminum foam, as a middle part, is modeled as a three-dimensional solid part. The aluminum foam is used to reduce the energy or absorb the blast energy through its compression. To model aluminum foam or metal foam behavior, the Crushable foam material model is selected. To model ceramic behavior under severe load, the ductile damage criterion, Drucker-Prager plasticity, and the equation of state are used. By using the material data, Abaqus can represent a good behavior of the ceramic. The dynamic explicit step in three separate simulations is used. In the first simulation, the analysis is done and the results are imported to the new or in the second simulation as an initial condition, and the results of the second one are also imported to the third simulation. In all of the simulations, the amount and the location of the TNT are changeable. The ideal or perfect contact is assumed between ceramic and aluminum foam. The CONWEP air blast procedure is selected to model the TNT detonation in all three analyses. The fixed boundary condition is assigned to all sides of the panel. The mesh should be fine to obtain correct results.

Example-10: Dynamic response of square sandwich plates with a metal foam core subjected to rigid projectile impact
In this lesson, the dynamic response of square sandwich plates with a metal foam core subjected to rigid projectile impact in Abaqus is studied. For the steel plate, the material with elastic-plastic(Johnson-Cook) is used. To model damage and failure of the steel plate, Johnson-Cook damage with evolution is implied. Abaqus/Explicit provides a dynamic failure model specifically for the Johnson-Cook plasticity model, which is suitable only for high-strain-rate deformation of metals. This model is referred to as the “Johnson-Cook dynamic failure model. Abaqus/Explicit also offers a more general implementation of the Johnson-Cook failure model as part of the family of damage initiation criteria, which is the recommended technique for modeling progressive damage and failure of materials. For the titanium foam, elastic data with Crushable foam plasticity, isotropic form with hardening data is used. For the aluminum, elastic, and Johnson-Cook plasticity and damage are considered. The dynamic explicit step is appropriate for this type of analysis. In this tutorial, the Dynamic response of square sandwich plates with a metal foam core subjected to rigid projectile impact in Abaqus has been investigated. The sandwich structure has been paid more attention to and widely used in a number of critical engineering applications due to its excellent advantages over the monolithic solid structure of the same mass. The sandwich structure has been considered to be a promising alternative to the monolithic solid structure. The structural behavior of the sandwich structure depends on the material properties, the geometries of the face-sheet, the core, and the boundary conditions, etc. Metal foam is a kind of lightweight material with a high stiffness-to-weight ratio, a high strength-to-weight ratio, novel physical and mechanical properties, such as nearly isotropic, high energy absorption, good sound damping, non-combustibility, easy fabrication to form curved configurations, and integrated face-sheets. The metal foam is then selected as the core of the sandwich structure.

Example-11: Finite Element Simulation of Titanium Foam Behavior for Dental Application
In this section, the Finite Element Simulation of Titanium Foam Behavior for Dental Application is investigated. In this simulation, the titanium foam implant and mandible are modeled as three-dimensional solid parts. The mandible contains cancellous and cortical bone. The titanium foam material is modeled as elastic with crushable foam plastic behavior. The isotropic type with hardening is used to model titanium foam material with a crushable foam model. The cancellous and cortical bone material is modeled as an elastic material. The dynamic explicit procedure is used to model the dynamic load over the titanium foam. In this tutorial, the finite element simulation of titanium foam behavior as an implant under dynamic load in Abaqus has been investigated. metal foams, new class materials, have increasingly been employed for a range of applications such as structural components, automotive parts, sound and vibration absorbers, heat exchangers, and biomedical implants. This is due to their unique combination of properties such as low density, high specific stiffness, high specific strength, and good energy absorption capability. Among metal foams, titanium foams (Ti-foams) are preferred in many crucial applications, including biomedical implants where biocompatibility is required. The main interests in using cellular metals come from the increase in the friction coefficient between the implant and the surrounding bone. It allows mechanical interlocking of bone with the implant by substantial bone ingrowth and better long-term stability. Additionally, the stiffness of the implants can be tailored by varying porosity to reduce the stress shielding effect

Example-12: Analysis of the steel bullet impact on the composite panel(Aluminum-Epoxy glue-Aluminum Foam)
In this lesson, the analysis of the steel bullet impact on the composite panel(Aluminum-Epoxy glue-Aluminum Foam) is studied. The steel bullet is modeled as a three-dimensional solid part. The aluminum sheet, Epoxy glue, and aluminum foam are modeled as three-dimensional solid parts. Currently, the usage of sandwich structures with a metal foam core is seeing increasing usage in different applications. From a structural point of view, in a sandwich structure, with metallic sheets and a metallic foam core, the foam is responsible for absorbing large amounts of energy when the structure is being plastically deformed. The foam core also provides good insulation against vibrations and contributes to the weight reduction of the product. structure. As a result, these materials are widely used in high-technology industries, such as the automotive and aerospatial industries. The aluminum foam material is modeled as Crushable foam plasticity in Abaqus. The isotropic plasticity with stress-strain hardening is used. The steel material is used for the bullet as an elastic-plastic material with Johnson-Cook damage criteria. The glue or cohesive interface is modeled as an elastic material type with traction and damage criteria. The aluminum face sheet is modeled as an elastic-plastic material with Johnson-Cook damage criteria to predict the failure zone. The dynamic explicit procedure is used to model the impact phenomena. The surface-to-surface contact with the contact property as a friction coefficient is used between the bullet and the aluminum sheet. The general contact algorithm with the contact property is used to consider all contacts of the parts. The contact between the aluminum sheet and glue, and the aluminum foam and glue, is considered a perfect contact.

Example-13: Dynamic response of aluminum foam core sandwich panels subjected to air blast loading
In this case, the dynamic response of aluminum foam core sandwich panels subjected to air blast loading is studied. In this tutorial, the Numerical analysis of the dynamic response of aluminum foam core sandwich panels subjected to air blast loading in Abaqus has been investigated. The two aluminum skin sheets are modeled as a three-dimensional solid part. The aluminum foam as the core is modeled as a three-dimensional solid part. The up-gradation of ship protection level attracted a great many attention from the naval departments and related scholars. The potential improvement by optimizing the design of a conventional stiffened plate has been exploited sufficiently for over a century. Therefore, it becomes impossible to meet the requirements of new weapon threats if the structural weight is limited. Cellular foam core sandwich structures, as a key member in the family of lightweight structures, are of current research and interest due to their high strength-to-weight ratio, stiffness-to-weight ratio, and superior energy absorption capability. Especially, the microstructure of foam cores endows them with the ability to undergo large plastic deformation under relatively long low plateau stress, and thus they could continue to exhibit excellent blast resistance before collapsing into a more stable state or fracture. Over the past few decades, extensive studies of cellular foam core sandwich structures have been reported on their dynamic responses under impact/blast loadings. In the numerical model, a Johnson-Cook material model available in Abaqus is employed to model the behavior of aluminum skin sheets. The Johnson-Cook damage is used to model damage and failure in the aluminum sheets. The Crushablefoam plasticity is used as an isotropic material with hardening. The dynamic explicit step is used to model the dynamic solution of the blasting procedure. The perfect contact is assumed between the aluminum foam and the aluminum sheets. The CONWEP blast procedure is used to model the detonation of TNT as an air blast technique.

Example-14: Bending behavior of aluminum foam-filled double cylindrical tubes
In this lesson, the bending behavior of aluminum foam-filled double cylindrical tubes is investigated. The two aluminum tubes are modeled as a three-dimensional shell part and foam as a solid part. Some rigid bodies are created as a hydraulic jack and a boundary area. The aluminum material is modeled as an elastic-plastic material with shear, ductile, and MSFLD damage criteria with evolution. The criterion can predict tube damage during dynamic bending. The foam material is modeled as an elastic material with Crashable foam plasticity coupled with hardening data. The dynamic explicit step is appropriate for this type of analysis. The general contact algorithm with a friction coefficient as a contact property is selected.

Example-15: Analysis of the three-point bending of a foam-filled aluminum tube under dynamic load
In this section, the analysis of the three-point bending of a foam-filled aluminum tube under dynamic load is investigated. The foam is modeled as a three-dimensional solid part, and the aluminum tube is modeled as a three-dimensional shell part. Three rigid bodies are used as a pusher and supporters. To model aluminum behavior under dynamic bending, elastic-plastic property with ductile, shear, and MSFLD damage is used. These parameters will provide a good behavior of aluminum if damage happens in the model. To model foam behavior, crashable foam plasticity with hardening is used. The dynamic explicit procedure is appropriate for this type of analysis. The contact between the aluminum tube and the foam is considered a perfect contact. The surface-to-surface contact with the property is considered for the rigid bodies' contact with the aluminum tube. In passenger cars, the side impact beam is used as the crashworthy structure, which strengthens the door of the vehicle and protects passengers from side collisions. Aluminum alloy tubes are mostly used as side-impact beams because of their improved strength-to-weight ratios, which is a key factor for fuel economy. Mostly metallic circular cylindrical aluminum alloy tubes are used as energy absorbers because of their low weight and ease of manufacturing process. The severity of the side collision in the passenger cars can be reduced by increasing the load-carrying capacity and energy absorption characteristics of the aluminum alloy tube.

Example-16: Crushing Simulation of Foam-Filled Aluminium Tubes
In this lesson, the Crushing Simulation of Foam-Filled Aluminium Tubes is demonstrated through a practical tutorial. Thin-walled metallic tubes have been applied as energy absorbers because of their progressive buckling under axial compressive loading and the lightness of the structure. According to previous investigations, thin-walled circular tubes can collapse in axisymmetric mode, also known as concertina or ring mode, non-axisymmetric mode, also known as diamond mode, or mixed mode. In which mode a tube crushes largely depends on the geometry of the tube. Energy will be absorbed through the progressive buckling of the structure. In this tutorial, axisymmetric dimension is used to model the 3-dimensional behavior of aluminum and foam. For the aluminum elastic-plastic material, and for the foam elastic and crushable foam behavior with hardening is used. The dynamic explicit procedure is appropriate for this type of analysis. The surface-to-surface contact algorithm to define interaction among all parts and self-contact to define the self-contact for aluminum and foam are used.

Example-17: Simulation of the foam-cored sandwich tubes subjected to internal air blast
In this lesson, the simulation of the foam-cored sandwich tubes subjected to internal air blast in Abaqus is done. Johnson-Cook plasticity for tubes and crushable foam with hardening for foam has been used to evaluate the compaction of foam and deformation of tubes. A dynamic explicit step is appropriate for this type of analysis. The contact between steel tubes and foam is considered as perfect contact, and the CONWEP air blast procedure has been selected to imply blast load over the internal surfaces. During the analysis, the blast causes a large deformation in the internal pipe, and this deformation causes a huge compaction of the foam part. Foams, a new class of ultra-light materials, can absorb a large amount of kinetic energy because of their ability to undergo large deformation at a nearly constant plateau stress. Foam-cored sandwich structures have received increasing attention because of their excellent property of withstanding blast loading, and have been extensively used in marine and other military applications. The remarkable performances of sandwich structures depend on the innovative geometrical design of the foam core. Furthermore, traditional blast-resistant devices perform with low efficiency and a heavy weight. Lightweight and improved blast-resistant containment vessels have become popular with the increase in terrorism. The sandwich tube has been considered a novel structural design that can enhance blast-resistant vessels to contain explosive materials and protect persons or equipment from internal explosions. The foam-cored sandwich tube has better energy absorption (EA) capability than the monolithic blast-resistant tube because the sandwich structures can undergo extreme plastic deformation at an almost constant plateau stress. The dynamic response of sandwich tubes has received increasing attention over the last decade.

Example-18: Modeling of the air blast load over a sandwich panel(GFRP+Foam)
In this case, the modeling of the air blast load over a sandwich panel(GFRP+Foam) in Abaqus is studied. Sandwich panels based on two relatively stiff face sheets separated by a foam core are commonplace in the marine industry, for example, in surfboard and yacht construction. Lightweight sandwich materials are attractive options for the transport industry, which is seeking to improve fuel economy and speed whilst reducing harmful emissions. At the same time, there is a competing requirement for vehicles to be protected from explosions, which traditionally involves the use of strong, relatively ductile metals such as armour steel. To model GFRP, Hashin’s damage criterion and for foam Crushable material model have been used. A dynamic explicit procedure is appropriate for this type of analysis. For modeling detonation behavior of TNT, the CONWEP procedure is selected, and during the analysis blast wave creates damage over the facial composite layouts, but after that, the foam core absorbs the detonation energy, and the back plate composites stay intact. The foam has a large deformation because of absorbs energy

Example-19: Analysis of the air blast analyses of insulated concrete sandwich panels using a unified non-linear finite element model
In this section, the analysis of the air blast analyses of insulated concrete sandwich panels using a unified non-linear finite element model is investigated. To model the concrete and foam solid part, the frontal and shear FRP shell part, and to model beam wire part are used. CDP model for concrete, crushable foam for foam, Johnson-Cook plasticity for beam, and Hashin’s damage for composite are used. The Dynamic Explicit procedure is appropriate for this type of analysis. The contact between concrete-FRP and concrete-foam is considered ideal, and CONWEP interaction has been used to model blast wave distribution. Insulated concrete sandwich panels are comprised of two outer concrete wythes and an inner layer of foam insulation. They have been increasingly used because of their advantages of light weight and energy efficiency. Various shear connectors can be used to connect the two outer concrete wythes. More recently, Fiber-Reinforced Polymer (FRP) shear connectors have been used, which can eliminate thermal bridging and improve the thermal performance.Insulated concrete sandwich panels are comprised of two layers of concrete, known as wythes, separated by a layer of rigid foam plastic insulation. The two wythes are connected by some form of shear transferring mechanism, generally using solid concrete web zones, metal connectors, plastic connectors, or a combination of these elements. The panels can provide a dual function of transferring load and insulating the structure, among other desirable characteristics of normal concrete panels, such as durability

Example-20: Simulation of the CEL explosion over the composite foam-insulated concrete sandwich panels
In this lesson, the simulation of the CEL explosion over the composite foam-insulated concrete sandwich panels is demonstrated through a practical model. Two concrete layers at the front and back are modeled as a three-dimensional solid part. The foam inside those two layers is modeled as a three-dimensional part, and the beam as reinforcement inside the concrete is modeled as a wire part. The TNT is modeled as a sphere, and the Eulerian domain as an Eulerian part. To model the TNT behavior JWL equation of state is used. The Jones-Wilkens-Lee (or JWL) equation of state models the pressure generated by the release of chemical energy in an explosive. This model is implemented in a form referred to as a programmed burn, which means that the reaction and initiation of the explosive are not determined by shock in the material. Instead, the initiation time is determined by a geometric construction using the detonation wave speed and the distance of the material point from the detonation points. To model foam behavior, crashable foam plasticity with hardening is used. The crushable foam model with volumetric hardening uses a yield surface with an elliptical dependence of deviatoric stress on pressure stress. It assumes that the evolution of the yield surface is controlled by the volumetric compacting plastic strain experienced by the material. To model concrete behavior under a massive pressure load, the Johnson-Holmquist model is used, and for a steel beam, Johnson-Cook plasticity and damage are used. The dynamic explicit step is appropriate for this type of analysis. The interaction between concrete slabs and foam is considered as perfect contact, and for all parts in the Eulerian domain, the general contact with property has been selected. The beam parts are embedded inside the concrete's host.

Reviews

No Review Yet

29 people watching this product now!

Related Products

Cohesive modeling of fracture in asphalt mixtures at low temperatures

Abaqus

Mastering Simulation with Simulink

MATLAB

Tunnel and TBM Analysis and Simulation Package in Abaqus

Abaqus

Welding Analysis and Simulation Package in Abaqus

Abaqus

Soil Analysis package

Abaqus

VDload Subroutine for Movement of a Train on Railroad

Abaqus

Analysis and Validation of a Composite Pressure Vessel for Liquefied Ammonia Storage

Abaqus

Wrist joint with an implant – FE model

Abaqus

Polymer and Metal Foam Analysis Package in Abaqus

Material Includes

Audience

What You Will Learn?

About Course

📘 Introduction to Polymer and Metal Foam Analysis

1. Metal and Polymer foam

2. Why Analyze Them Together?

3. Key Analysis Challenges

4. Simulation in Abaqus

5. Applications in Industry

Course Content

Abaqus Files

Document

Tutorial Video

Aabqus Files

Document

Tutorial Video

Abaqus Files

Document

Tutorial Video

Abaqus Files

Document

Tutorial Video

Abaqus Files

Document

Tutorial Video

Abaqus Files

Document

Tutorial Video

Abaqus Files

Document

Tutorial Video

Abaqus Files

Document

Tutorial Video

Abaqus Files

Document

Tutorial Video

Abaqus Files

Document

Tutorial Video

Abaqus Files

Document

Tutroial Video

Abaqus Files

Document

Tutorial Video

Abaqus Files

Document

Tutorial Video

Abaqus Files

Document

Tutorial Video

Abaqus Files

Document

Tutorial Video

Abaqus Files

Document

Tutorial Video

Aabqus Files

Document

Tutorial Video

Abaqus Files

Tutorial Video

Abaqus Files

Document

Tutorial Video

Abaqus Files

Document

Tutorial Video-1

Tutorial Video-2

Reviews

Student Ratings & Reviews

Material Includes

Audience

Related Products