Engineering Downloads

Let’s Learn and Collaborate

Engineering Downloads

Register | Login

Masonry Wall Analysis Package in Abaqus

  • Categories: Abaqus, Concrete structure, Course, Earthquake and Seismic, Explosion, Finite Element, Masonry structure, Seismic Analysis, Structures
Masonry Wall analysis and Structure Package in Abaqus
Masonry Wall and Structure Package in Abaqus
Masonry Wall and Structure Package in Abaqus
Masonry Wall and Structure Package in Abaqus
4a19242c-8cde-45af-8e03-08529bf9c0cb

Peyman Karampour
€154,00 €298,00
  • Level
    Intermediate
  • Duration
    4 hours 45 minutes
  • Last Updated
    August 28, 2025
€154,00 €298,00
  • Lifetime access
  • Download capability
5 people watching this product now!

Material Includes

  • 1- Abaqus Files
  • 2- Document+Paper
  • 3- Tutorial Videos

Audience

  • 1- Mechanical Engineering
  • 2- Civil Engineering
  • 3- Structural Engineering
  • 4- Military and Defense Engineering
  • 5- Earthquake Engineering

What You Will Learn?

  • In this course, you'll learn all about masonry walls in Abaqus through 10 practical tutorials. Static and dynamic analysis, explosion, compression, seismic model, earthquake load, masonry wall with FRP reinforcement, macro, micro, and semi-micro model, CDP material model, cohesive interaction, and more are available in this package.

About Course

📌 Introduction to Masonry Wall Analysis and Simulation

Masonry walls have been used for centuries as load-bearing and non-load-bearing structural components in buildings. They are typically constructed from bricks, blocks, or stones bonded with mortar, forming a composite material system. While masonry is durable and economical, its structural behavior is complex due to its heterogeneous, anisotropic, and brittle nature.

This package everything about masonry wall through 10 comprehensive tutorials. 

1. Why Analysis is Important

  • Structural Safety: Masonry walls often resist vertical loads (gravity) and lateral loads (wind, earthquake). Proper analysis ensures stability and safety.
  • Performance Assessment: Engineers need to predict strength, stiffness, and failure modes.
  • Retrofitting & Rehabilitation: Old masonry structures often require evaluation before strengthening.

2. Challenges in Masonry Analysis

  • Masonry is a non-homogeneous material, consisting of units (such as brick/block/stone) and mortar joints with varying mechanical properties.
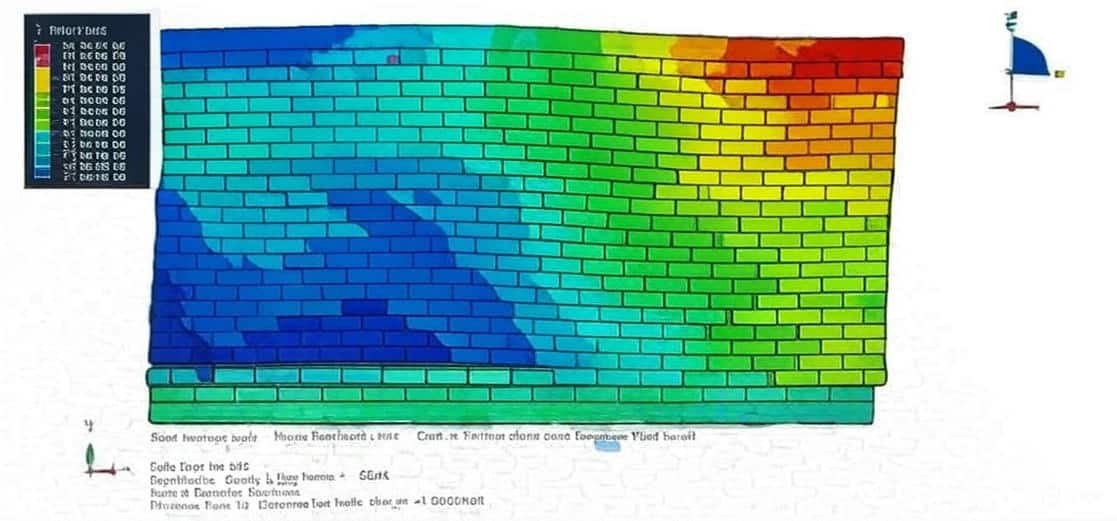
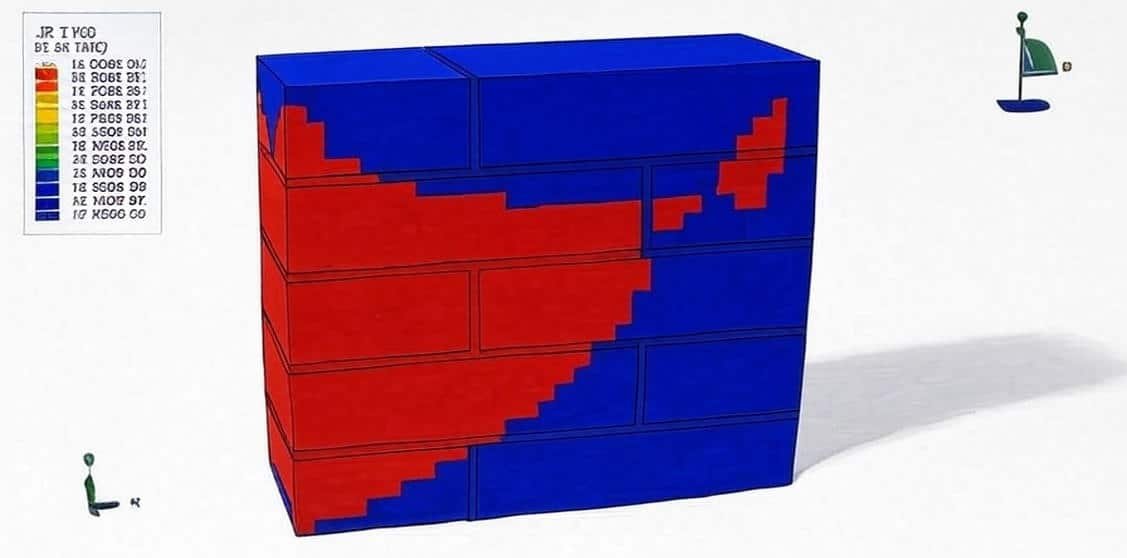
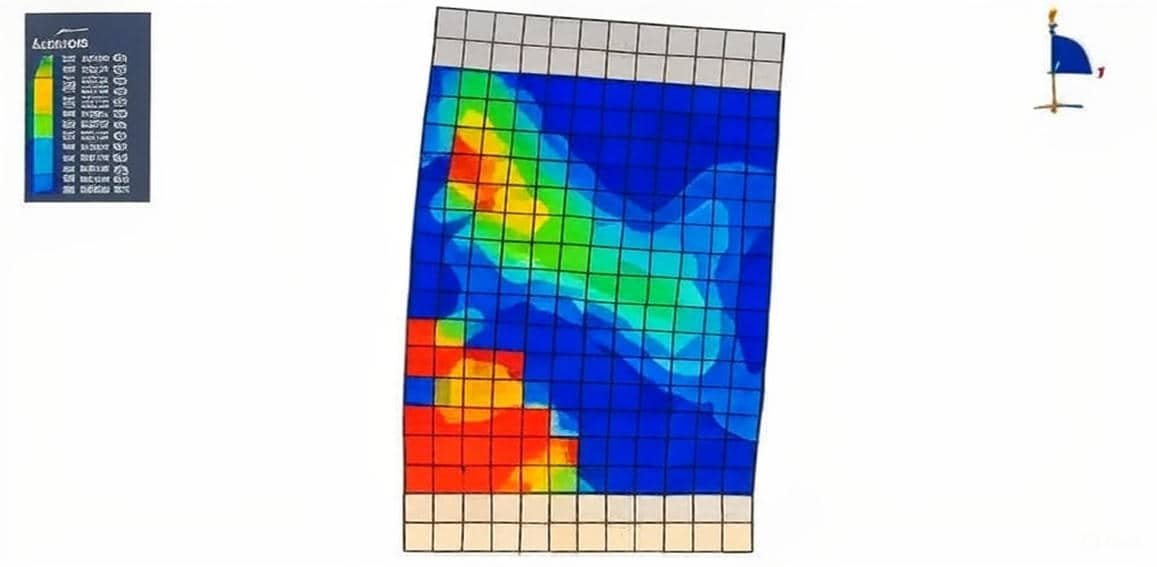
  • Nonlinear behavior: Masonry tends to crack, crush, or lose bond under stress.
  • Anisotropy: Properties vary in horizontal and vertical directions due to joint alignment.

3. Approaches to Masonry Wall Analysis

  • Empirical/Code-based methods: Simplified equations based on experiments and building codes (e.g., Eurocode 6, ACI 530, IS 1905).
  • Analytical models:
    • Equivalent Frame Method (EFM): Walls modeled as piers and spandrels with nonlinear springs.
    • Macro-modeling: Masonry treated as a homogenized continuum with averaged properties.
    • Micro-modeling: Units, mortar, and interface are explicitly modeled to capture cracks and bond failures.
  • Numerical Simulation:
    • Finite Element Method (FEM): Widely used for both macro and micro approaches.
    • Discrete Element Method (DEM): Models masonry as rigid blocks connected by contacts.
    • Hybrid FEM-DEM methods: Capture both continuum stresses and discrete cracking.

4. Simulation Goals

  • Load-bearing capacity: Vertical compressive strength, in-plane and out-of-plane bending.
  • Seismic performance: Nonlinear dynamic analysis to predict cracking, rocking, and collapse.
  • Failure mechanisms: Diagonal shear cracking, sliding at mortar joints, and corner crushing.
  • Retrofitting effectiveness: FRP wrapping, grouting, or confinement simulation.

👉 In summary, masonry wall analysis and simulation aim to realistically predict the mechanical response and failure of masonry under various loads. Due to its brittle and composite nature, engineers often balance between simplified analytical models (for practicality) and advanced numerical simulations (for detailed insight).

Show more
Show less

Course Content

Example-1: Semi-micro modeling of the masonry wall(brick wall) Rocking mode
In this lesson, the semi-micro modeling of the masonry wall(brick wall), Rocking mode, in Abaqus is studied. Masonry is the oldest structural material still in use for a vast variety of construction. It has been continually employed for different construction purposes. Old masonry structures were designed and constructed without any complicated mathematics, but through the expert masons, with trial-and-error methods. In the last few decades, engineers’ attention has been devoted to the new methods of analysis of masonry structures. Overall, to capture the response of masonry more realistically, a numerical model requires interface elements. One possible option is to use interface elements for the joints and a suitable model for masonry units, grout, and mortars. To model the behavior of mortar, there are two ways. The first way defines the mortar as a three-dimensional part and assigns material as a traction separation law because during analysis mortar experienced damage, and it should be considered. The second way uses cohesive behavior coupled with damage and evolution and assigns it to the interaction surfaces between bricks. In this simulation, the second way has been used, and BK low is considered for it as a damage formulation with normal, shear, and tangential stiffness.

  • Abaqus Files
  • Document
  • Tutorial Video
    28:07

Example-2: Static modeling of the masonry wall(brick+mortar) under compression load
In this section, the static modeling of the masonry wall(brick+mortar) under compression load in Abaqus is investigated. Mortar is modeled as a three-dimensional solid part. Bricks are modeled as three-dimensional solid parts. To model the behavior of bricks and mortar, elastic and plastic data are selected. The general static step is appropriate for this type of analysis. Masonry wall systems are building systems that use masonry materials such as brick, stone, or concrete blocks to construct walls. These materials are typically stacked on top of each other and held together with mortar. Masonry is the oldest technique used for constructing buildings or structures. Stress analysis of a brick-mortar is analyzed during this tutorial. Structural engineers use specified civil engineering standards during the design process of any object. These standards comprise the majority of building cases; however, for complex and unusual buildings, the structural engineers can use a numerical analysis of the structure. For sufficient analysis of the structure and approved material, it is necessary to apply a proper material model in the numerical analysis. Masonry structures are a challenge for engineers during the design process of complex objects due to the visible layered structure of the material. The use of an adequate model in this case is crucial. The majority of existing and historic masonry structures are composed of regularly or semi-regularly arranged clay or stone units, bound through the use of mortar. The complexity of the structural behavior of masonry arises from the dimension ratios of the members, the brittle behavior of its constituent materials in tension and shear, and the geometrical complexity of the bond patterns.

Example-3: Macro-modeling of the masonry wall under compression and transverse load
In this case, the macro-modeling of the masonry wall under compression and transverse load in Abaqus is done through a practical tutorial. The wall is modeled as a three-dimensional solid part. The beam is modeled as a three-dimensional solid part. In the early stages of masonry structures, designs were normally based on a great exact insight without scientific or prescient techniques. It is still broadly utilized because of its ease of construction and simplicity, with low material expense and more aesthetics. Masonry structures are a composite of two different materials,i.e., bricks and mortar, in which blocks (a building unit made of any specific material, e.g., brick) are laid upon each other with binder or cohesive material, i.e., mortar, in between them. Materials are distinguished from each other by their mechanical properties and have different responses to loading. Brick masonry is used in structures due to its load transfer mechanism, but it has poor performance and needs confinement when subjected to in-plane lateral loading. This behavior causes damage to the masonry, and its response towards such loading has to be measured experimentally and numerically to get benefits from the masonry. The concrete damaged plasticity model is used to model the plastic behavior of the masonry wall. The elastic material model is selected for the beam. The dynamic explicit step is appropriate for this type of analysis. In this tutorial, two dynamic steps are used. In the first step, the compression load is applied to the top surface of the upper beam, and in the second step, the lateral load as a displacement is assigned to the top beam.

Example-4: Numerical simulation of reinforced brick masonry beams using GFRP reinforcement
In this lesson, the numerical simulation of reinforced brick masonry beams using GFRP reinforcement in Abaqus is studied. The bricks are modeled as three-dimensional solid parts, and GFRP sheets are modeled as three-dimensional shell parts. The elastic behavior with Concrete Damaged Plasticity is used for the bricks. The elastic behavior lamina type with Hashin’s damage criterion is used for the GFRP sheets. The explicit step with the general contact is used. The contact between blocks and the GFRP sheet is assumed as perfect contact. The mortar is used as a cohesive surface interaction by using cohesive behavior and damage parameters. Natural stone structures represent the largest part of the construction heritage in the world, such as bridges, civil and worship buildings, or historical monuments. The natural stone is preferred for many reasons, such as beauty, accessibility, hardness, durability, strength, and sustainability. It is necessary to have a good understanding of the mechanical behavior of stone structures. Their main characteristics are high compressive strength and almost null tensile strength due to the joints. Therefore, in historical structures, the use of stone is mostly restricted to members mainly working in compression. The reinforcement of masonry structures is one of the most frequently used practices in the restoration of historical buildings to enhance their resistance. It can be performed using steel bars, rings, and/or composite materials. In the last two decades, composite materials, like FRP, have been increasingly considered for strengthening and repairing both modern and historic masonry constructions. FRP is are excellent candidate for strengthening because of the high tensile strength they provide, their resistance to corrosion, and their easy handling. Several papers have addressed the strengthening of masonry with carbon and glass fiber-reinforced composites.

Example-5: Analysis of the infill masonry wall in two steel columns under vertical and transverse load
In this section, the analysis of the infill masonry wall in two steel columns under vertical and transverse load in Abaqus is investigated through a comprehensive tutorial. Masonry structures are among the most common types of buildings, being economical and easily made. The possibility of using conventional materials, the easy method of construction, and the lower level of construction expertise needed are characteristics of masonry structures. However, they are brittle structures because of the fragile nature of the materials and elements used in their construction. Numerous masonry structures are found across famous city centres, rural regions, and mountainous parts of different countries such as the southern USA, Iran, Europe, the Middle East, Australia, and New Zealand. The brick is modeled as a three-dimensional part, the concrete beam as a three-dimensional solid part, and the steel columns as a three-dimensional shell part. In this micro modeling is used to simulate the interaction between bricks and define the mortar among them. The Concrete damage plasticity for bricks, the elastic model for concrete beam, and the elastic-plastic behavior for steel column are used as a material model definition. The dynamic explicit step is appropriate for this type of analysis. The mortar is used as interaction behavior by using the friction coefficient, hard contact as normal behavior, cohesive specification as three stiffness factors, and damage with evolution. In this way, Abaqus can consider the mortar among the bricks as a cohesive surface interaction. The fixed boundary condition is assigned to the bottom surfaces of the wall and columns. The pressure load is applied to the upper concrete beam, and the transvers concentrated load is applied to the steel column.

Exampe-6: Simulation of the CEL explosion near a masonry wall
In this case, the simulation of the CEL explosion near a masonry wall is done in Abaqus. The concrete bricks are modeled as a dimensional part, and TNT as a solid, and the domain as an Eulerian part. The primary aim of this work is to obtain a reliable numerical model of a masonry wall that reflects the behavior of a real structure subjected to a CEL explosion. The damage parameter for the masonry wall is another crucial factor in this simulation. To model concrete blocks under high strain rates. Johnson-Holmquist model is used. The JWL equation of state to model TNT behavior is implied. A dynamic explicit procedure with general contact is used. To model mortar behavior in interaction, the cohesive property as cohesive, damage with evolution, and tangential friction are used. Numerical simulations are used extensively for solving a vast variety of dynamic problems associated with explosions, such as gaseous or condensed charge detonations followed by pressure wave propagation through the ambient air. Utilizing these methods, it is possible to evaluate the propagation direction of this pressure wave and its effect on different construction structures. For many decades, researchers have been conducting and presenting numerous and real-life experiments along with numerical explosive simulations for different types of materials in an attempt to capture the detailed mechanism of the blast phenomenon and obtain credible numerical modelling methods in order to predict the response and final failure of the obstacles. The behavior of a structure subjected to an explosion depends on the type and power of the charge. Varying these two elements causes fundamentally different results. The current study includes the motivation for undertaking such a subject and presents the state of the art in the area of interest.

Example-7: Simulation of the earthquake load over a masonry wall(concrete brick)
In this lesson, the simulation of the earthquake load over a masonry wall(concrete brick) in Abaqus is studied. The concrete bricks and concrete columns are modeled as three-dimensional parts. The recent rise in terrorist activities around the globe has attracted the attention of engineers and scientists towards the vulnerability of buildings and infrastructure to blast loads. The consequent effects of these loads may range from minor damage to structural collapse, accompanied by huge loss of life. The masonry, which is the oldest and the most widely used building material, either in masonry buildings or in the form of infill walls in reinforced concrete (RC) framed buildings, suffers the most damage. Even if there is no complete damage or structural collapse, the flying debris may cause significant loss of life or injuries. As a result, efforts were made by several investigators to examine feasible methods for strengthening masonry walls in order to enhance their resistance to blast loads. Although several techniques have been tried but one of the most popular methods of retrofitting unreinforced masonry (URM) walls is the application of fiber-reinforced polymers (FRP) to its surface. As the blast causes a pressure to be exerted on the surface of a wall, the flexural resistance of the wall needs to be enhanced.

Example-8: Air blast explosion analysis near a masonry wall
In this section, the air blast explosion analysis near a masonry wall is investigated. In this simulation Elastic brick model and the CDP concrete brick model have been used. The first file ended successfully, but in the second case to the accumulation of tensile and compressive damage, the wall failed. To model the behavior of mortar, there are two ways. The first way defines the mortar as a three-dimensional part and assigns material as a traction separation law because during analysis mortar experienced damage, and it should be considered. The second way uses cohesive behavior coupled with damage and evolution and assigns it to the interaction surfaces between bricks. In this simulation, the second way has been used, and the BK law is considered for it as a damage formulation with normal, shear, and tangential stiffness. Recent terrorist attacks not only targeted government buildings, but also some random civilian structures such as hotels, shopping centers, and traffic stations. This imposes a great challenge on attack prevention since it is impractical to deny public access to these structures. Once a terrorist attack is not successfully prevented and occurs in the near field of the building structures, serious casualties are not the only result from the explosion itself, but also from the high-speed ejecting fragments discharging from the locally damaged structural and building envelope. And owing to the ease of construction and low costs, clay masonry is commonly used in China and other countries as building envelope materials besides concrete masonry and glass. However, this clay masonry, which is made of clay bricks and mortar, tends to break into sharp fragments due to its brittle nature and low integrity under close-in explosions, inevitably causing casualties and injuries to occupants and severe damage to the equipment or furniture inside the room. Thus, there is an urgent need to study the behavior of local damage, as well as the fragment characteristics of unreinforced masonry walls under near-field explosions for blast protection against such a hazard. With the popularization of natural gas used in the industrial and civilian fields, gas explosion accidents have been reported frequently, causing massive damage and structural failure. In order to reduce the potential hazards to structures and enhance the safety of properties and human lives, it is necessary to investigate the dynamic response and failure mechanism of masonry walls under blast explosions.

Example-9: Analysis of the masonry wall with FRP as reinforcement under pressure and transverse load
In this lesson, the analysis of the masonry wall with FRP as reinforcement under pressure and transverse load is considered. In this simulation, three three-dimensional spaces to model bricks have been used. Materials for concrete and bricks are considered elastic materials. To model the behavior of mortar, there are two ways. The first way defines the mortar as a three-dimensional part and assigns material as a traction separation law because during analysis mortar experienced damage, and it should be considered. The second way uses cohesive behavior coupled with damage and evolution and assigns it to the interaction surfaces between bricks. In this simulation, the second way has been used, and the BK law is considered for it as a damage formulation with normal, shear, and tangential stiffness. During the analysis by applying normal pressure and a transverse concentrated force, a rocking failure mode appears, but in the second case with FRP reinforcement, the wall overcomes rocking failure.

Example-10: Analysis of the SPH explosion over a masonry wall
In this case, the analysis of the SPH explosion over a masonry wall in Abaqus is investigated. The wall is modeled with concrete bricks and a concrete beam as three-dimensional parts. The TNT part is modeled as a sphere solid part. To model the correct behavior of concrete blocks under huge pressure over a short time, it is necessary to use a proper material model instead of CDP and the Brittle cracking model. For TNT JWL equation of state has been used. The Jones-Wilkens-Lee (or JWL) equation of state models the pressure generated by the release of chemical energy in an explosive. This model is implemented in a form referred to as a programmed burn, which means that the reaction and initiation of the explosive is not determined by shock in the material. Instead, the initiation time is determined by a geometric construction using the detonation wave speed and the distance of the material point from the detonation points. A dynamic explicit procedure is appropriate for this type of analysis. The mortar between blocks has been modeled as an interaction property between surfaces, like cohesive behavior, damage, and evolution.

Reviews

Student Ratings & Reviews

No Review Yet
No Review Yet
€154,00 €298,00
  • Lifetime access
  • Download capability
5 people watching this product now!

Material Includes

  • 1- Abaqus Files
  • 2- Document+Paper
  • 3- Tutorial Videos

Audience

  • 1- Mechanical Engineering
  • 2- Civil Engineering
  • 3- Structural Engineering
  • 4- Military and Defense Engineering
  • 5- Earthquake Engineering

Related  Products

Abaqus simulation of bonding mechanism in cold gas spraying with particle impact and critical velocity results
Bonding mechanism in cold gas spraying

Abaqus

View details
Masonry Wall analysis and Structure Package in Abaqus
Masonry Wall Analysis Package in Abaqus

Abaqus

View details
Bolt Analysis Package in Abaqus
Bolt Analysis Package in Abaqus

Abaqus

View details
Labyrinthine acoustic metamaterial design
Labyrinthine Acoustic Metamaterial: Sound Transmission Loss and Dispersion Curve

Acoustics

View details
Wood Analysis Package in Abaqus
Wood Analysis Package in Abaqus

Abaqus

View details
Core-shell drug delivery modeling in COMSOL
drug delivery

COMSOL Multiphysics

View details
Dam Analysis Package
Dam Analysis Package(Explosion, Earthquake, and Crack)

Abaqus

View details
Buckling of laminate composites FEA
Buckling analysis of laminate composites and testing its validity

Abaqus

View details

See more

Want to receive push notifications for all major on-site activities?

✕