

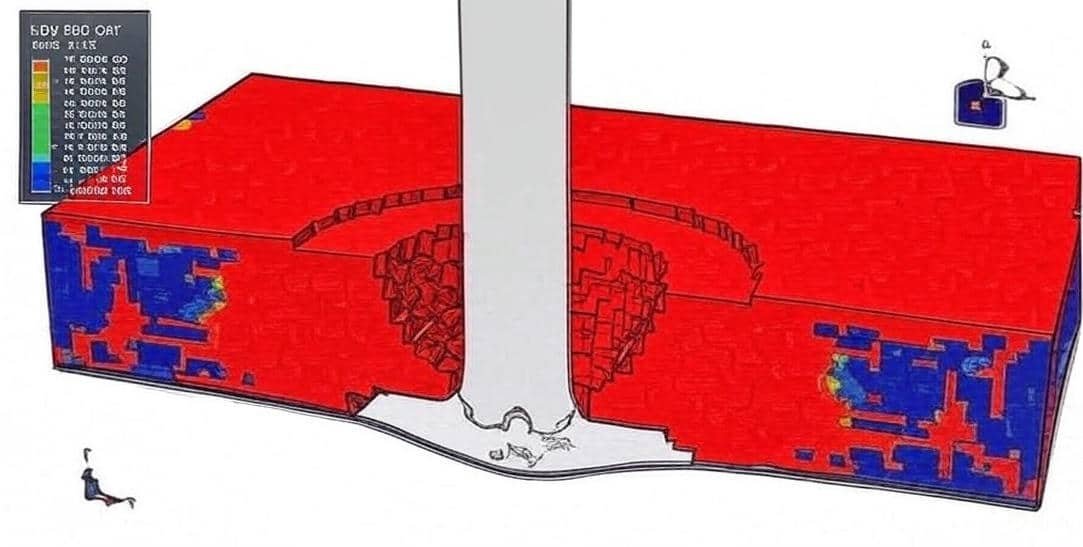
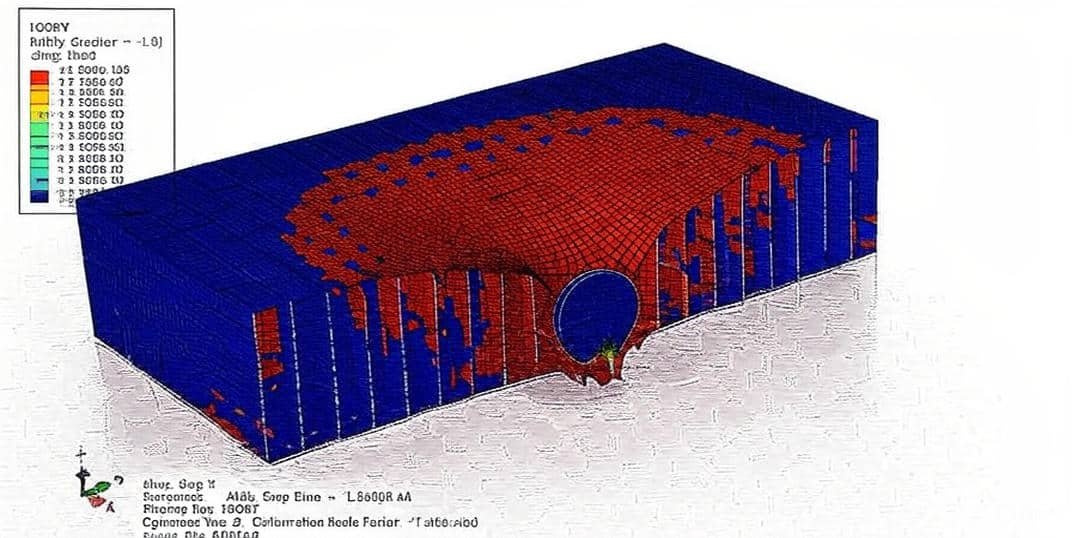
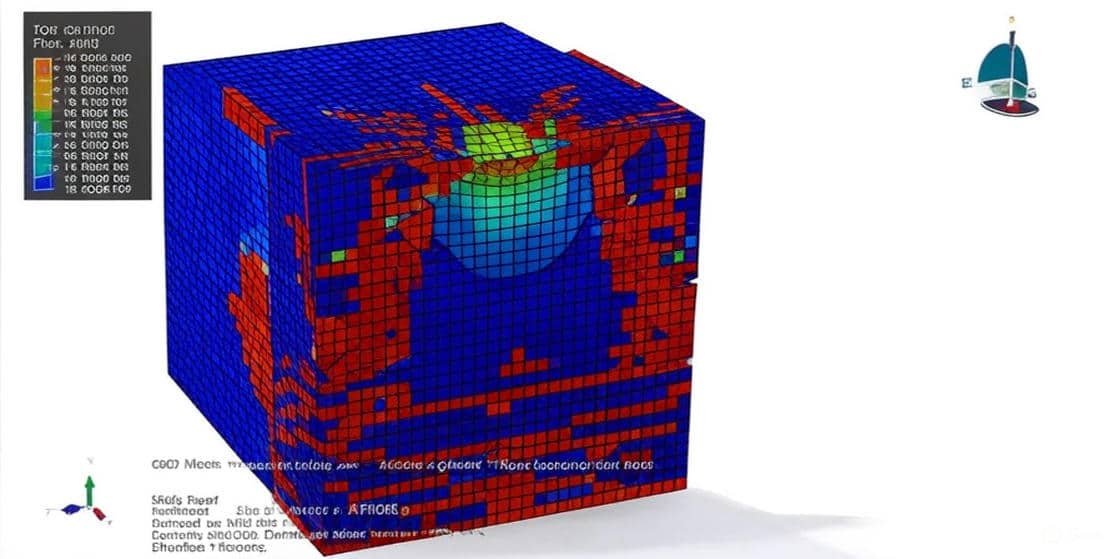
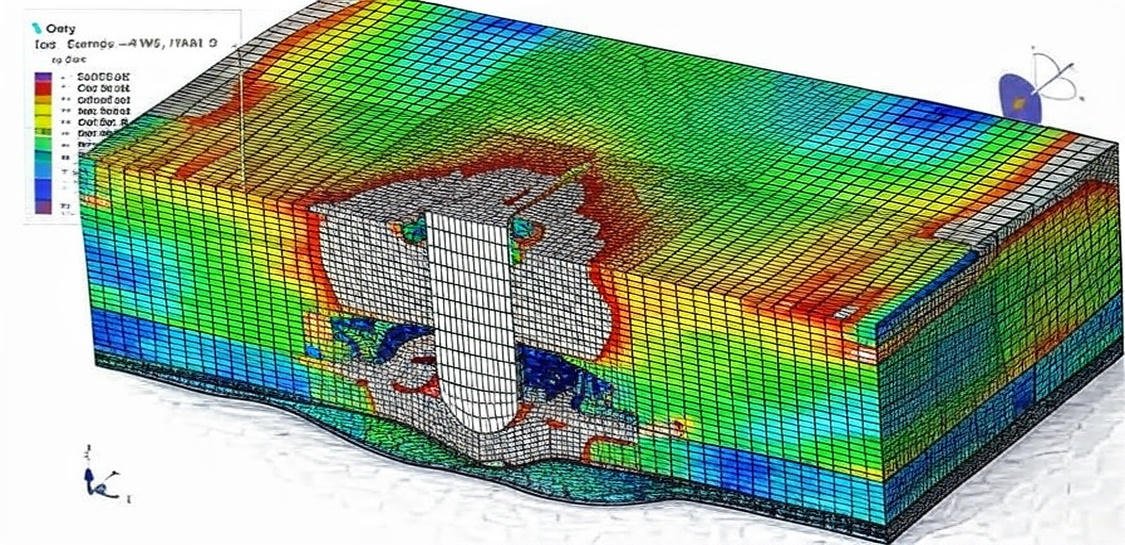
This course offers an in-depth study of impact dynamics and numerical simulation using Abaqus. It is designed to provide students, researchers, and practicing engineers with both theoretical understanding and practical skills in modeling a wide range of impact scenarios. Through systematically structured examples, participants will learn to model and analyze high-velocity and low-velocity impacts on various materials and structures, including ceramics, metals, composites, polymers, reinforced concrete, protective panels, and fluid-structure systems.
The course emphasizes:
Fundamental principles of impact mechanics and material behavior under dynamic loading.
Practical simulation techniques for setting up impact problems in Abaqus.
Advanced applications, including ballistic impacts, multi-layered armor systems, fluid cavity interactions, and reinforced structural components.
Comparative studies of different materials and structural configurations to evaluate performance under impact loading.
By working through over 35 detailed case studies, participants will gain hands-on experience with real-world problems, ranging from projectile penetration and ballistic resistance to low-speed structural impacts and repeated load scenarios. The course thus bridges the gap between theoretical knowledge and engineering practice, preparing learners to apply advanced finite element modeling techniques to research, design, and industrial problem-solving in the fields of aerospace, defense, civil, and mechanical engineering.

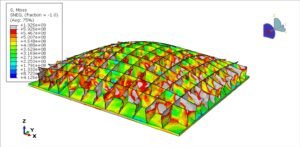
Abaqus
€68,00 €34,00
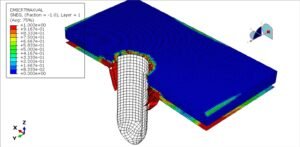
Abaqus
€77,00 €39,00
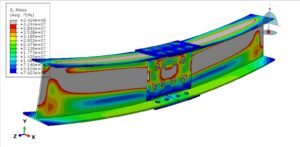
Abaqus
€79,00 €39,00
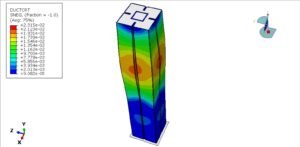
Abaqus
€75,00 €37,00

Abaqus
€76,00 €38,00
Abaqus
€79,00 €38,00
See more

Want to receive push notifications for all major on-site activities?