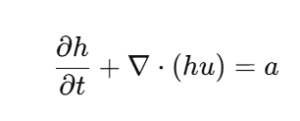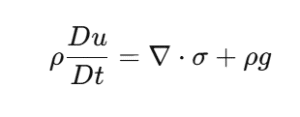What is Ice Modeling and Simulation?

Ice modeling and simulation is the computational study of how ice forms, evolves, moves, and interacts with its environment. It combines physics, mathematics, and computational methods to predict ice behavior in natural and engineered systems.

Applications span:

• Climate science – modeling polar ice sheets and sea ice to predict sea-level rise.
• Engineering – designing ships, offshore platforms, and wind turbines for icy conditions.
• Glaciology – studying glacier dynamics and ice–bedrock interaction.
• Planetary science – modeling ice on Mars, Europa, or Enceladus.

Core Physical Processes

Any realistic ice simulation must account for multiple interlinked phenomena:

a. Thermodynamics of Ice

• Phase changes – freezing, melting, sublimation.
• Heat transfer – conduction within ice, convection with surrounding fluids, radiation balance.
• Salinity effects – for sea ice, salt content changes freezing/melting points.

b. Mechanical Behavior

• Viscoelastic and viscoplastic deformation – ice can flow like a slow liquid (creep) or fracture like a brittle solid.
• Fracture and ridging – sea ice forms pressure ridges; glacier ice can calve into icebergs.
• Stress–strain relationships – Glen’s flow law is widely used for glacier ice.

c. Environmental Coupling

• Interaction with ocean currents (thermohaline circulation, wave action).
• Interaction with the atmosphere (winds, precipitation, temperature).
• Feedback loops in climate systems (albedo effect, heat fluxes).

Mathematical Framework

Ice modeling typically involves partial differential equations (PDEs) derived from:

• Mass conservation:

  where h is ice thickness, u is velocity, and a is accumulation/melt rate.

• Momentum conservation (Navier–Stokes adaptations for ice rheology): where σ is the stress tensor, g is the gravity.
• Energy conservation (heat equation with phase change terms).

These are often nonlinear and require numerical methods for solutions.

Modeling Approaches

Different levels of complexity are used depending on goals and computational resources:

1. Empirical / Statistical Models – fit to observational data; used for short-term forecasts.
2. Continuum Models – treat ice as a continuous medium, commonly used in climate models.
3. Discrete Element Models – represent ice as particles or blocks; good for fracture simulations.
4. Coupled Models – integrate ice with atmosphere–ocean systems for climate simulations.

Computational Techniques

Common numerical methods include:

• Finite difference and finite volume methods – for grid-based PDE solutions.
• Finite element methods (FEM) – good for complex geometries.
• Smoothed particle hydrodynamics (SPH) – for free-surface and fracture modeling.
• Level set or phase-field methods – for tracking ice–water boundaries.

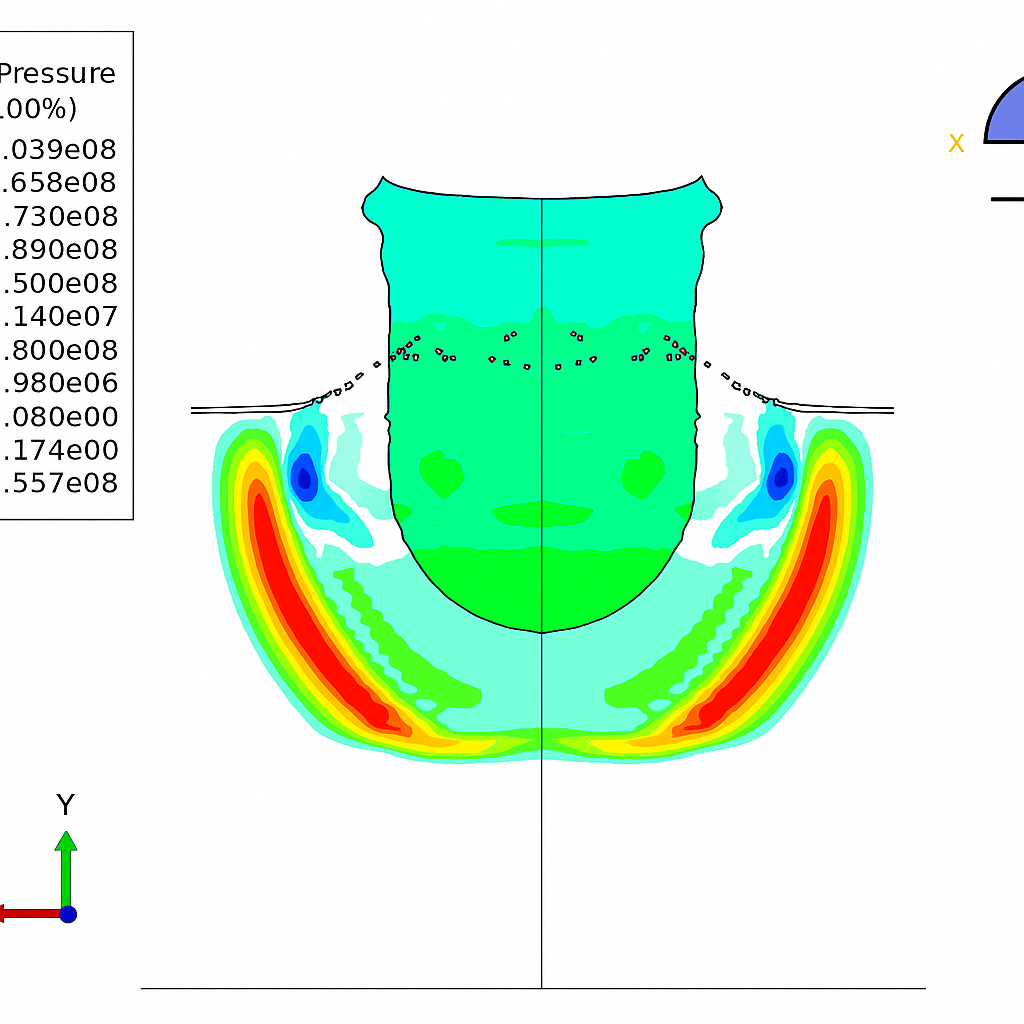
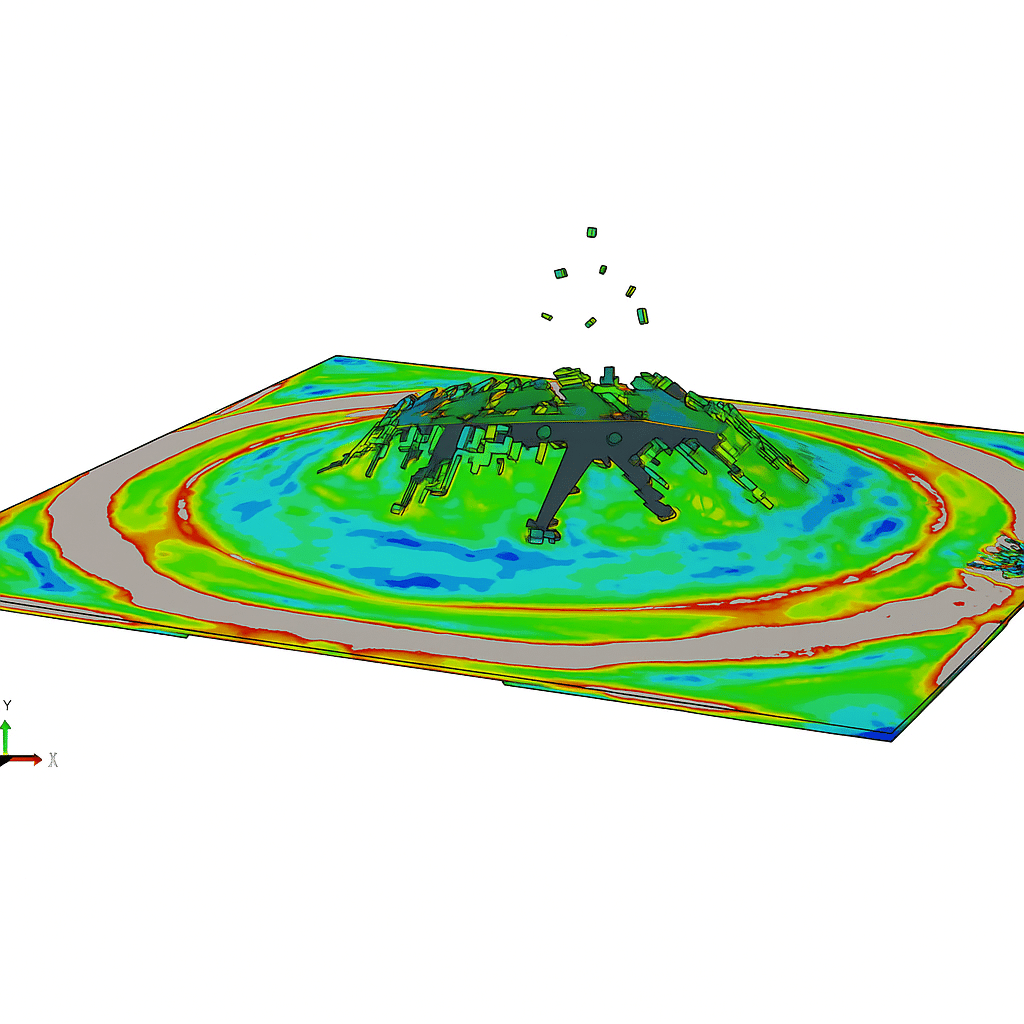
The JH-2 model (short for Johnson–Holmquist 2) is a constitutive model originally developed for brittle materials, like ceramics, rock, and concrete, to predict their behavior under high pressures, shear strains, and strain rates. It captures both the strength increase under compression and progressive damage due to fracturing.

Ice exhibits brittle fracture behavior, strain-rate dependence, and pressure sensitivity, characteristics well encapsulated by the JH-2 framework. By calibrating the model’s material constants to ice-specific behavior (e.g., texture, temperature, strain-rate), one can simulate realistic responses of ice under dynamic loads such as impacts or collisions.