

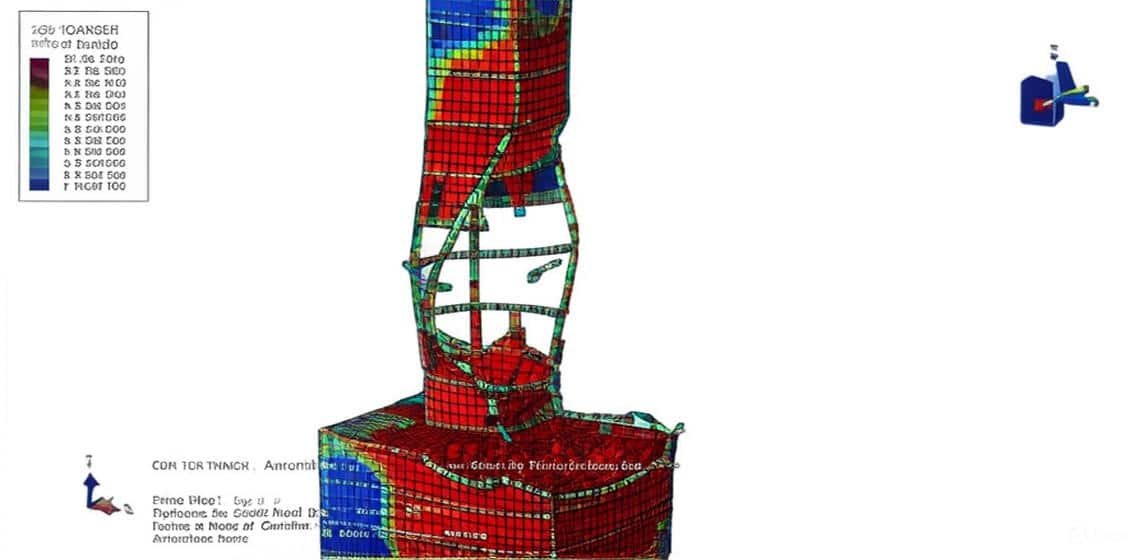
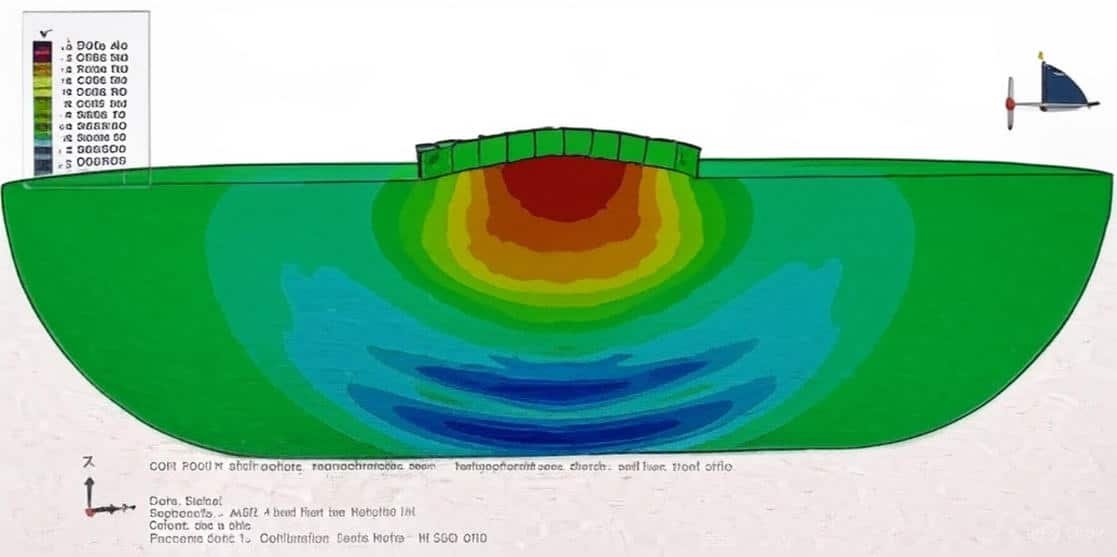
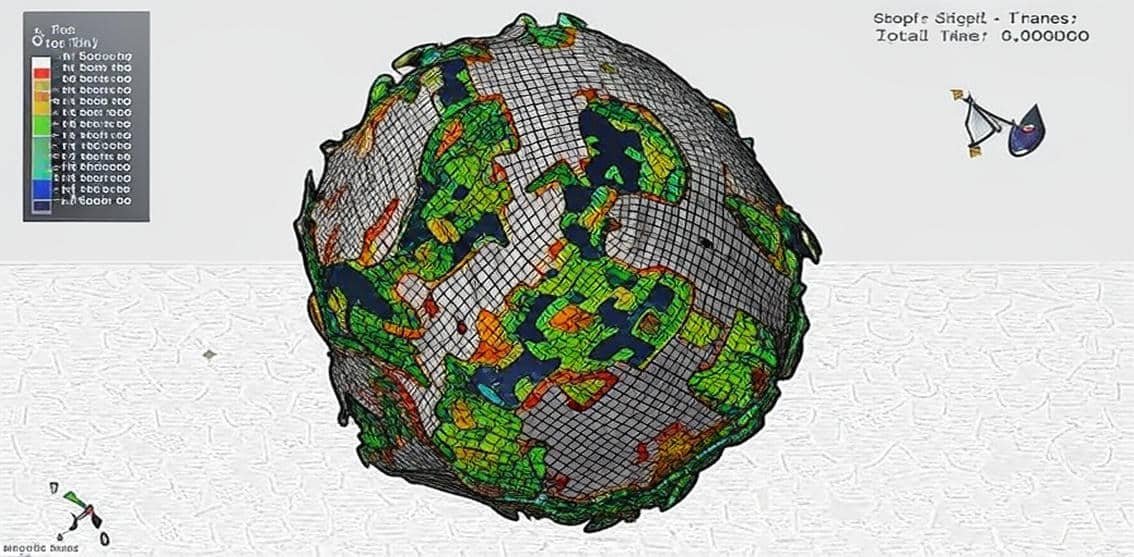
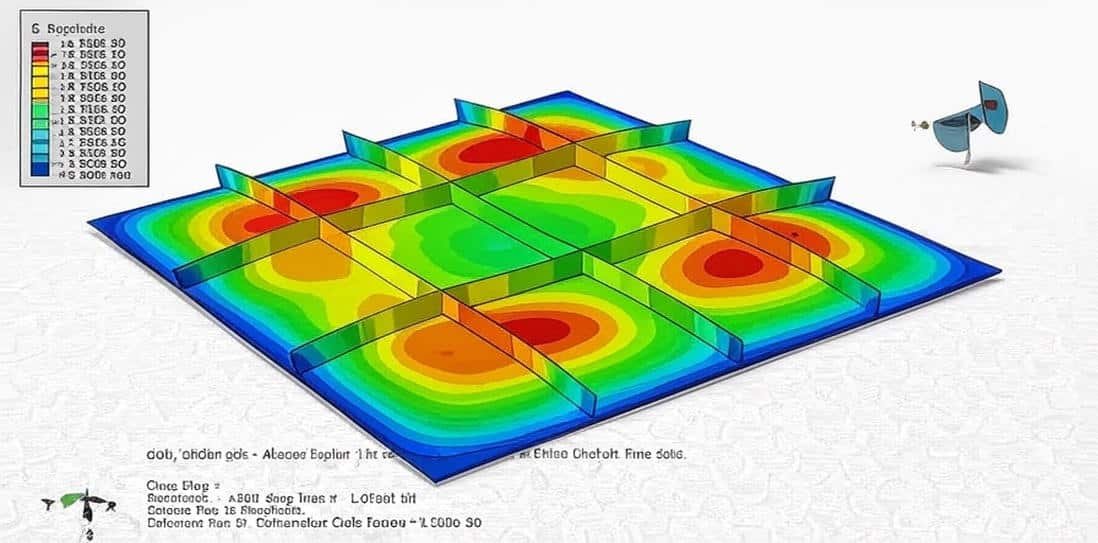
Explosions are highly transient, nonlinear events that involve rapid energy release, shock wave propagation, and complex interactions with surrounding media and structures. Modeling these phenomena is essential for applications in structural safety, defense engineering, energy systems, and disaster prevention. Because of their complexity, explosions are studied using advanced numerical methods that can accurately capture both the physics of detonation and the structural responses that follow.
This course provides a comprehensive, hands-on introduction to explosion modeling, guiding learners through a series of real-world examples that progressively build knowledge and skills. Starting with underground and underwater explosions, participants will learn to simulate cratering effects, shock transmission through soil and water, and the structural impact on tunnels, pipelines, and plates. The course then explores structural blast effects, covering reinforced concrete beams, columns, walls, and composite materials under blast loading.
A major focus is placed on advanced computational methods:
Coupled Eulerian–Lagrangian (CEL) simulations for soil–structure and blast–structure interaction.
Eulerian approaches for fluid–structure coupling in underwater explosions.
Smoothed Particle Hydrodynamics (SPH) for high-deformation and fracture modeling in concrete and masonry.
Acoustic and hybrid methods for large-scale explosion environments, such as dams and open-water conditions.
By the end of the course, participants will be able to:
Develop accurate models of explosions in different environments (underground, underwater, and air blasts).
Analyze the effects of explosions on various structures, including reinforced concrete, steel pipelines, masonry walls, and composite systems.
Select and apply the most suitable numerical method (CEL, Eulerian, SPH, or hybrid) for a given explosion problem.
Interpret results to inform engineering design, safety assessment, and mitigation strategies.
This course is designed for engineers, researchers, and students interested in computational mechanics, structural engineering, and blast dynamics, providing both theoretical insights and practical simulation skills.

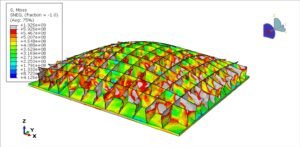
Abaqus
€68,00 €34,00
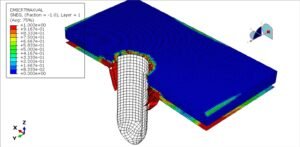
Abaqus
€77,00 €39,00
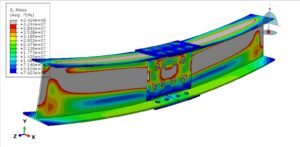
Abaqus
€79,00 €39,00
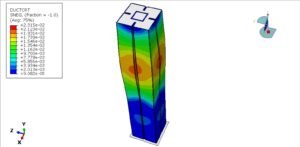
Abaqus
€75,00 €37,00

Abaqus
€76,00 €38,00
Abaqus
€79,00 €38,00
See more

Want to receive push notifications for all major on-site activities?