

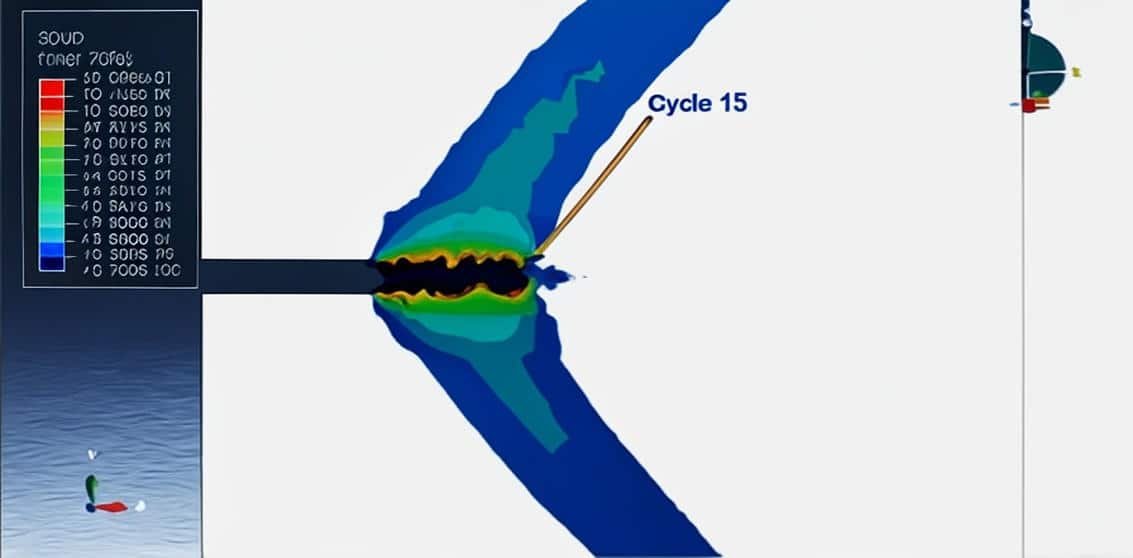
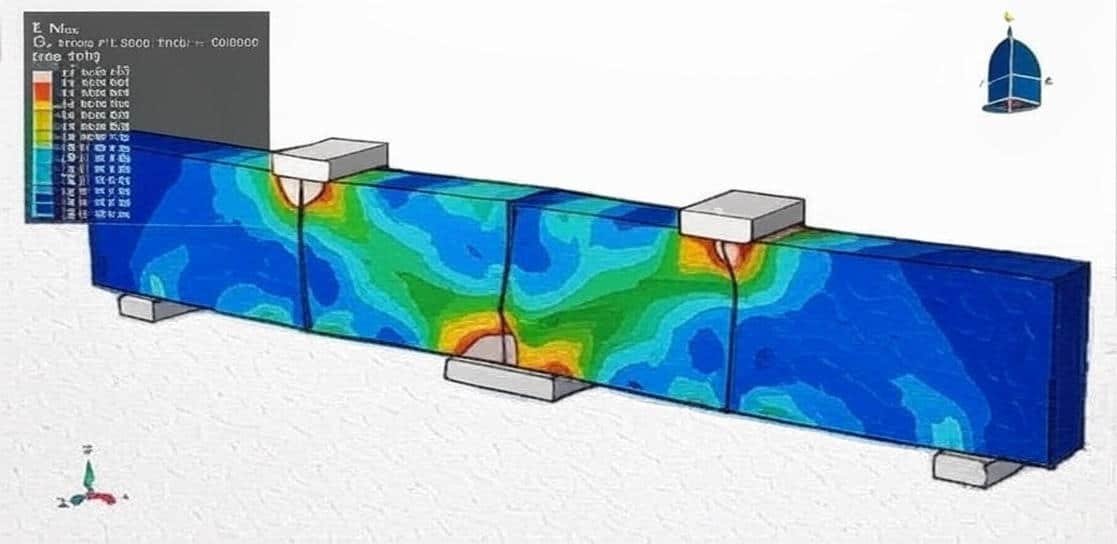


This course provides a comprehensive study of fatigue, fracture mechanics, and crack propagation, with emphasis on computational modeling and simulation. Students will learn how cracks initiate, grow, and interact with different loading conditions and materials, from metals to concrete and composite structures.
The curriculum progresses from fundamental fatigue and crack growth analyses in steel plates and pressure vessels to advanced XFEM-based simulations for concrete, wood, and reinforced structures. Key applications include bending tests, crack growth in reinforced concrete beams and walls, and large-scale fracture scenarios such as dam failure under pressure and load.
By combining theory, fracture mechanics principles, and simulation techniques, participants will develop the ability to:
Analyze fatigue life and crack growth in metals and reinforced materials.
Apply extended finite element methods (XFEM) to model crack propagation.
Evaluate structural safety under axial, bending, and pressure loads.
Simulate large-scale fracture processes in engineering structures.
This course equips learners with the analytical and practical skills needed to model, predict, and assess structural integrity across a wide range of engineering applications.

Abaqus
€68,00 €34,00
Abaqus
€77,00 €39,00
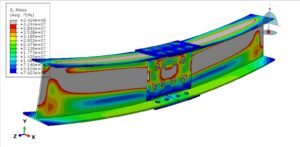
Abaqus
€79,00 €39,00
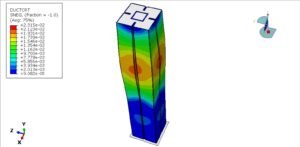
Abaqus
€75,00 €37,00

Abaqus
€76,00 €38,00
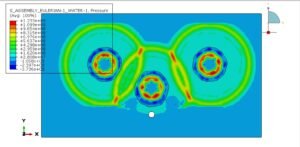
Abaqus
€79,00 €38,00
See more

Want to receive push notifications for all major on-site activities?