
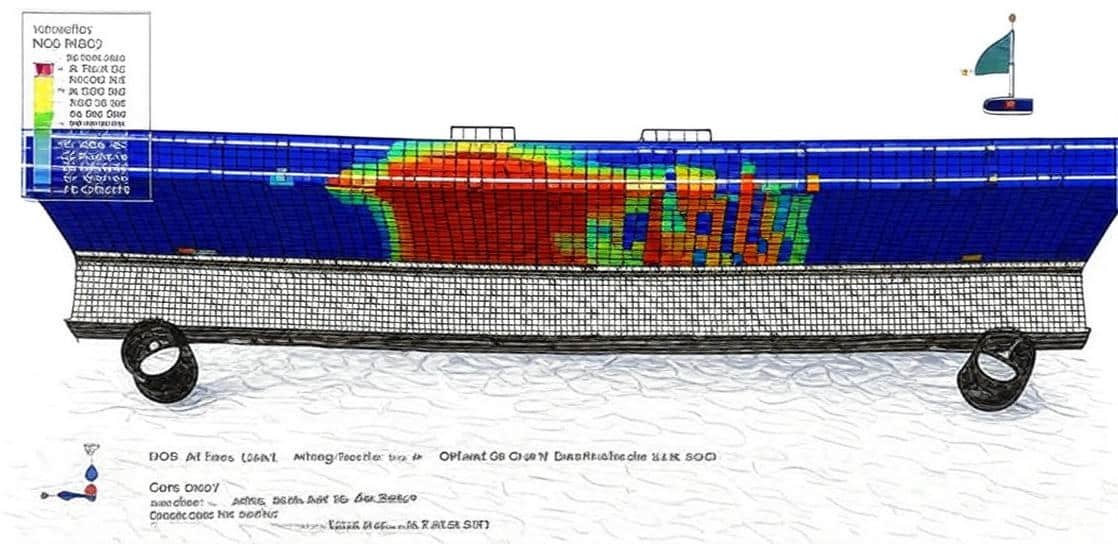
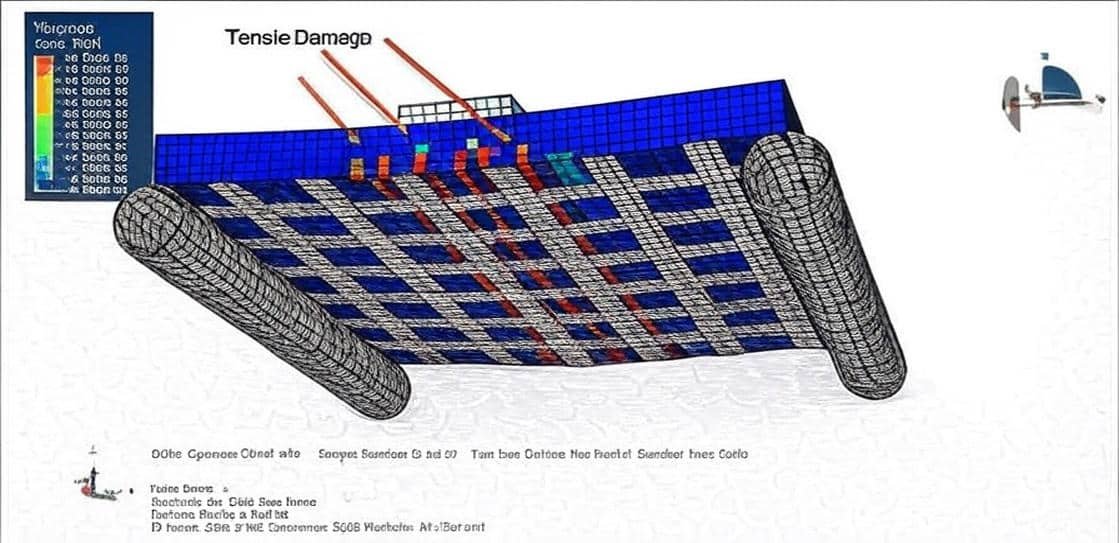
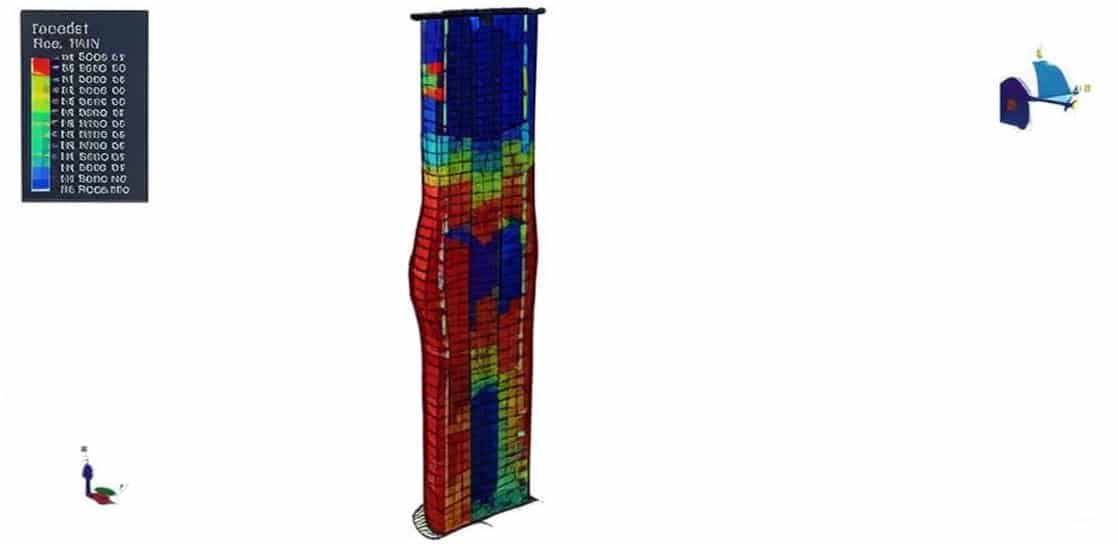
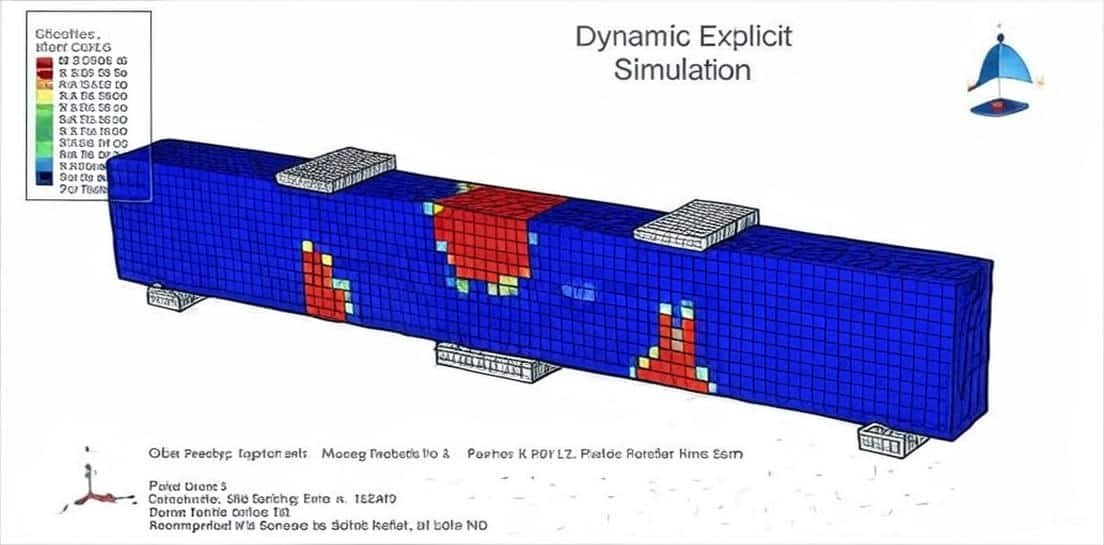
The study of concrete and composite structures plays a crucial role in modern structural engineering, particularly in designing resilient, high-performance buildings and infrastructure. Over the years, various modeling techniques have been developed to understand the behavior of reinforced and non-reinforced concrete beams, columns, and joints under different loading conditions. These models help engineers predict structural responses such as bending, axial compression, fracture, and cyclic loading, enabling safer and more efficient designs.
This collection of examples highlights a wide range of structural modeling approaches, including:
Numerical and analytical modeling of reinforced concrete beams and columns.
Flexural and axial behavior analysis under different loading scenarios, such as three-point and four-point bending tests.
The use of advanced materials, including fiber-reinforced polymers (FRP), ultra-high-performance concrete (UHPC), and composite steel-concrete systems.
Analysis of concrete-filled steel tubular (CFST) structures, steel-concrete joints, and prefabricated elements.
Together, these examples provide a comprehensive overview of current practices and methodologies in structural modeling, offering valuable insights for both research and practical applications in civil and structural engineering.


Abaqus
€81,00 €39,00

Abaqus
€299,00 €249,00

Uncategorized
€95,00 €80,00
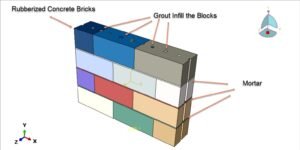
Abaqus
€79,00 €38,00
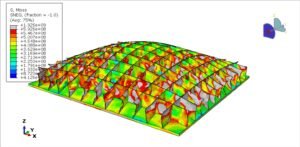
Abaqus
€68,00 €34,00
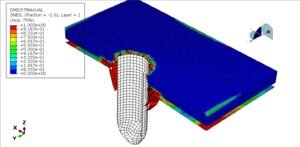
Abaqus
€77,00 €39,00
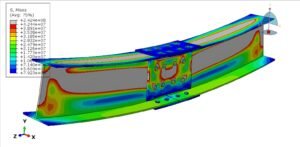
Abaqus
€79,00 €39,00
See more

Want to receive push notifications for all major on-site activities?