
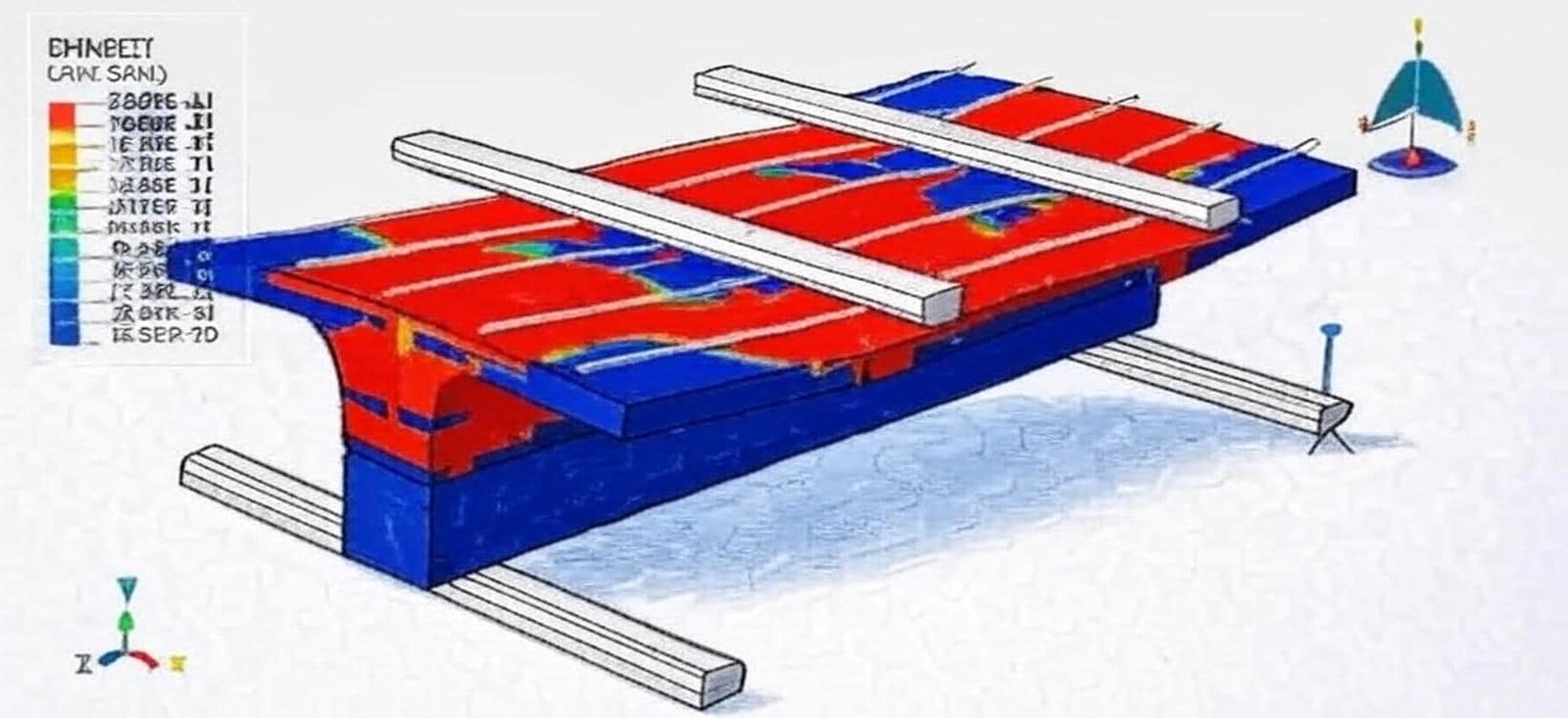
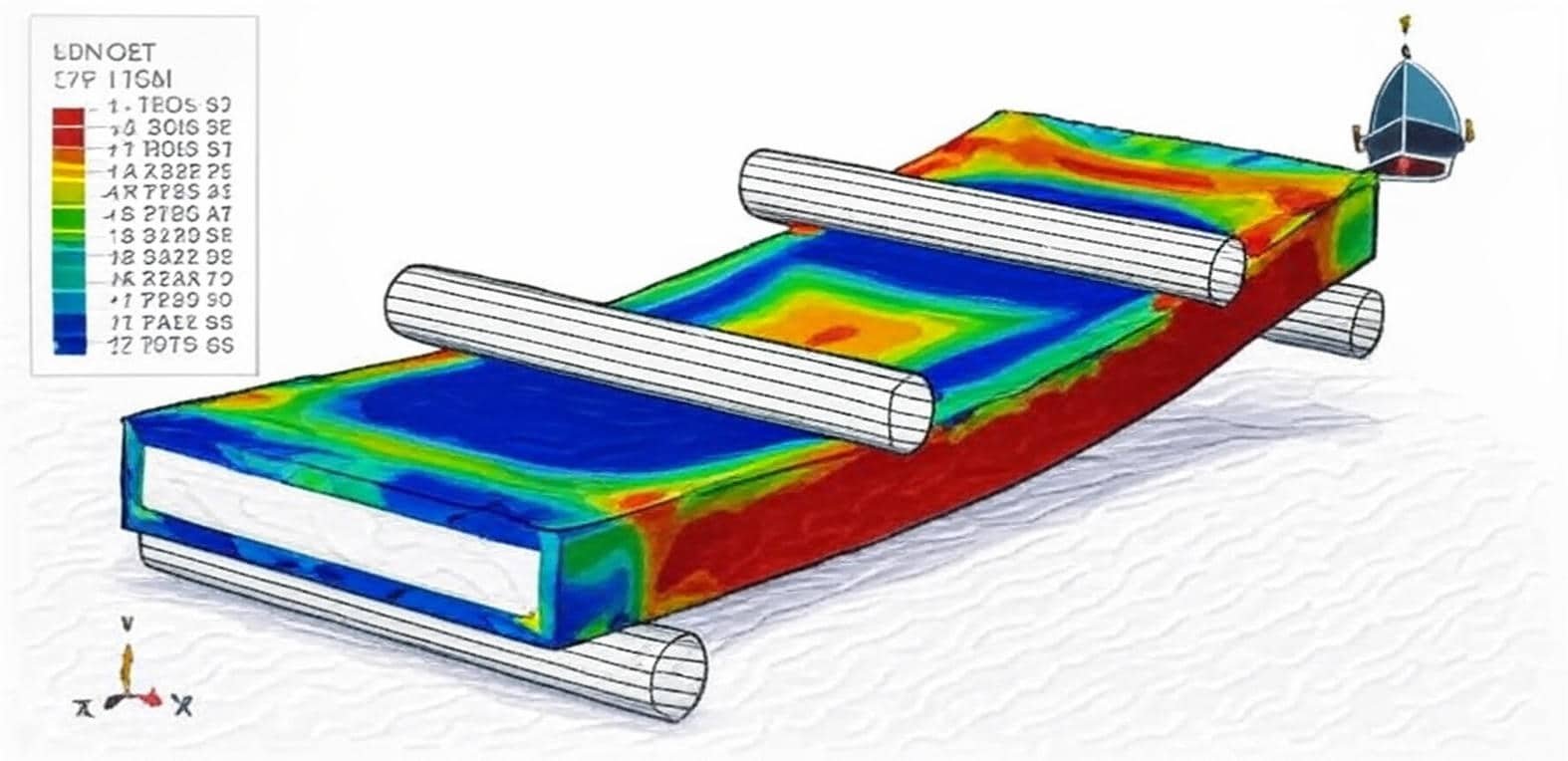
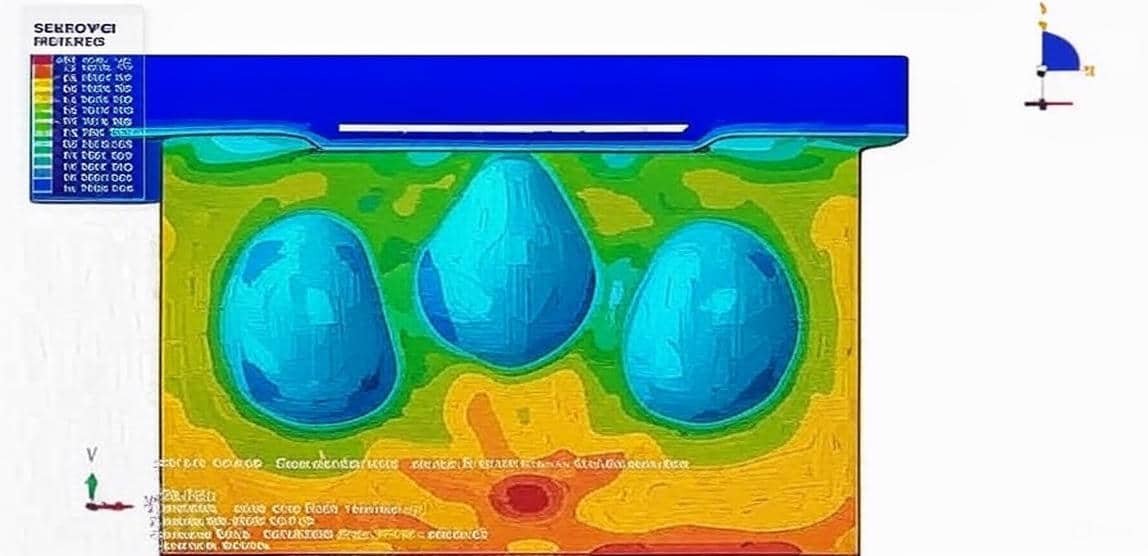

Concrete slabs are fundamental structural elements used in buildings, bridges, pavements, and industrial floors. They are designed to resist loads through a combination of bending, shear, and axial forces while ensuring adequate stiffness and serviceability. Because slabs are often subjected to complex loading and boundary conditions, analytical solutions can be difficult to obtain. As a result, numerical simulation has become an essential tool in the design and performance evaluation of concrete slabs.
This package includes 20 tutorials that cover all about concrete slabs, such as bending, four-point bending, bolted shear connectors in composite slab, concrete ribbed slab, blast loading, fire analysis, sequential CEL explosion, low-energy impact, interior voided RC slab, air blast, SPH explosion, UHPC slab, profiled steel deck composite slab, low-velocity impact, steel-concrete slab, and …
Finite Element Analysis (FEA), implemented in software such as Abaqus, enables engineers to model the nonlinear behavior of concrete, including cracking, crushing, creep, and reinforcement interaction. These simulations provide insights into stress distribution, deflection patterns, and failure mechanisms that are difficult to observe experimentally. Using the Concrete Slab Package in Abaqus, users can simulate various slab configurations—such as one-way or two-way slabs, flat plates, and ribbed slabs—under static, dynamic, or thermal loads.
Key objectives of concrete slab analysis and simulation include:
Evaluating load-bearing capacity and deflection performance.
Studying crack propagation and reinforcement effects.
Optimizing material usage and slab thickness for economy and sustainability.
Validating designs against relevant codes and standards (e.g., ACI, Eurocode).
Concrete slab analysis and simulation represent a crucial part of structural engineering research and design. By using advanced software like Abaqus, engineers can accurately model complex slab behaviors, reduce experimental costs, and improve design reliability. The integration of FEA results into design processes allows for the creation of more efficient, safe, and sustainable structures, aligning with modern engineering standards and sustainability goals.


Abaqus
€81,00 €39,00

Abaqus
€299,00 €249,00

Uncategorized
€95,00 €80,00
Abaqus
€79,00 €38,00
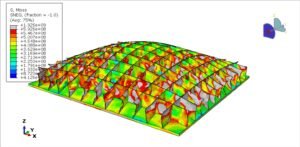
Abaqus
€68,00 €34,00
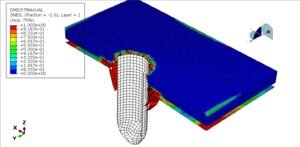
Abaqus
€77,00 €39,00
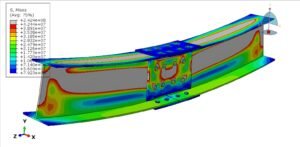
Abaqus
€79,00 €39,00
See more

Want to receive push notifications for all major on-site activities?