
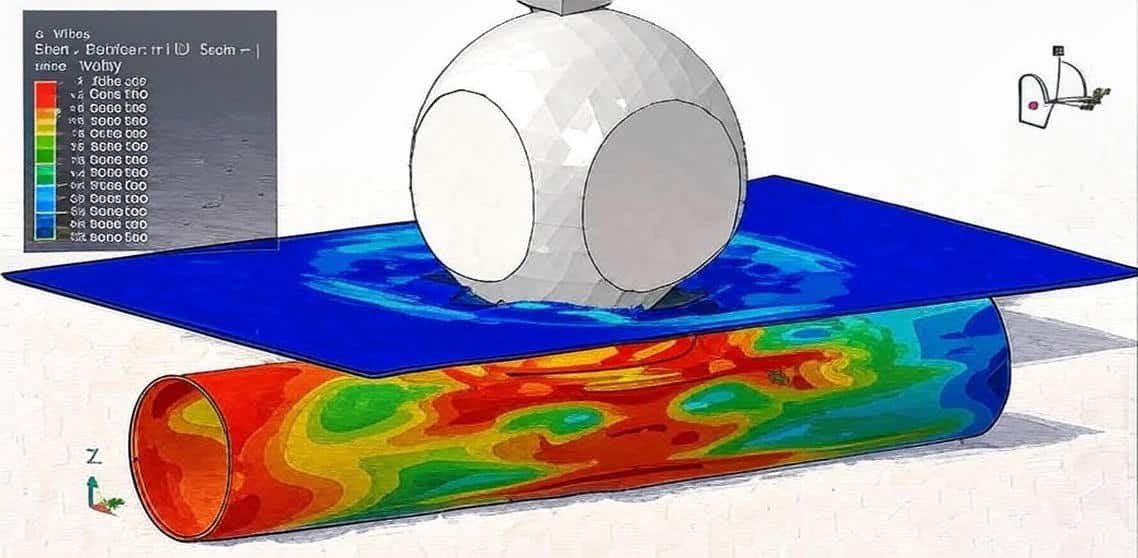

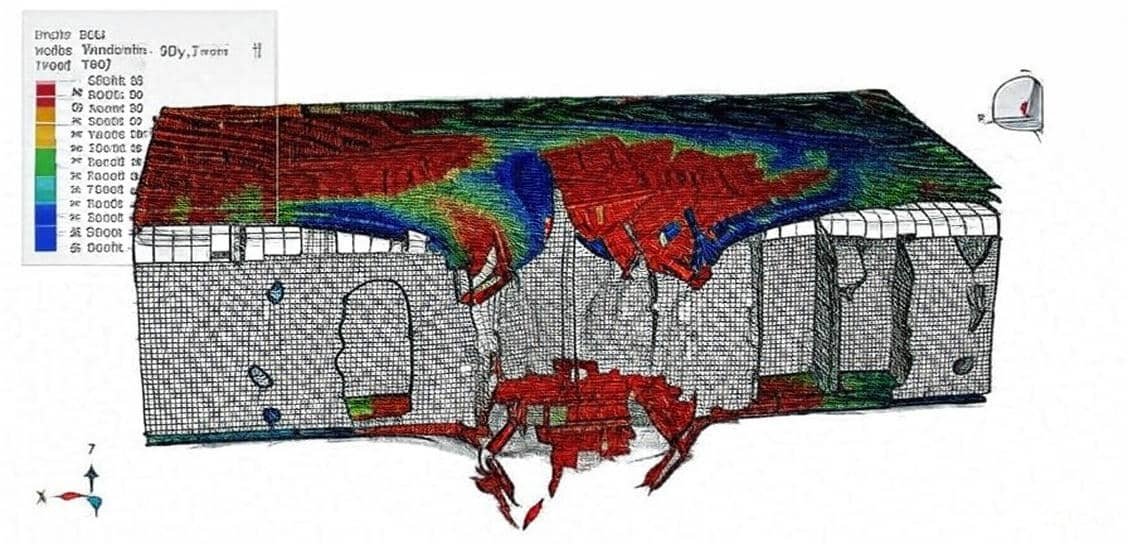

Composite materials are engineered by combining two or more constituent materials with different physical and chemical properties to achieve superior performance compared to their individual components. Typically, composites consist of a matrix material (such as a polymer, metal, or ceramic) reinforced with fibers or particles (such as carbon, glass, or aramid). The result is a lightweight yet strong material with enhanced stiffness, durability, and resistance to fatigue, making composites widely used in aerospace, automotive, marine, wind energy, and civil engineering applications.
This course includes 27 tutorials that cover all about composite materials like CFRP, GFRP, BFRP, AFRP, Banana-epoxy, jute-epoxy, green composite, bamboo fiber, and… in many simulations like high and low-velocity impact, blast, CEL explosion, bending, compression, cyclic loading, and …
Because of their heterogeneous and anisotropic nature, the behavior of composites under mechanical, thermal, and environmental loads is complex. Traditional analytical methods are often insufficient to capture these complexities. Therefore, numerical simulation tools—most notably the Finite Element Method (FEM)—are essential for understanding and predicting the performance of composite structures.
Composite material analysis and simulation involves:
Modern simulation software, such as Abaqus with the Composite Package, provides powerful tools for:
Summary:
In Abaqus, the method for composite material analysis involves defining anisotropic properties, building the ply layup, using appropriate elements, applying loads and failure criteria, and running progressive damage simulations. This allows engineers to predict the strength, stiffness, delamination, and ultimate failure of composite structures with high accuracy.
By integrating material modeling, structural mechanics, and computational simulation, engineers and researchers can design safer, lighter, and more cost-efficient composite structures while minimizing the need for expensive experimental testing.


Abaqus
€81,00 €39,00

Abaqus
€299,00 €249,00

Uncategorized
€95,00 €80,00
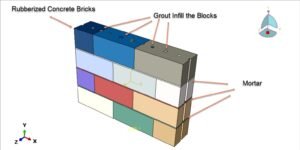
Abaqus
€79,00 €38,00
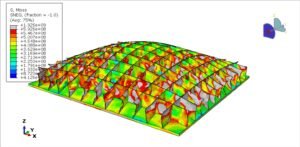
Abaqus
€68,00 €34,00
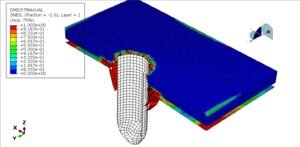
Abaqus
€77,00 €39,00
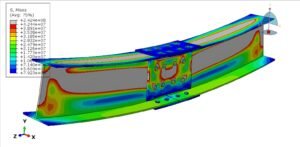
Abaqus
€79,00 €39,00
See more

Want to receive push notifications for all major on-site activities?