Paper abstract

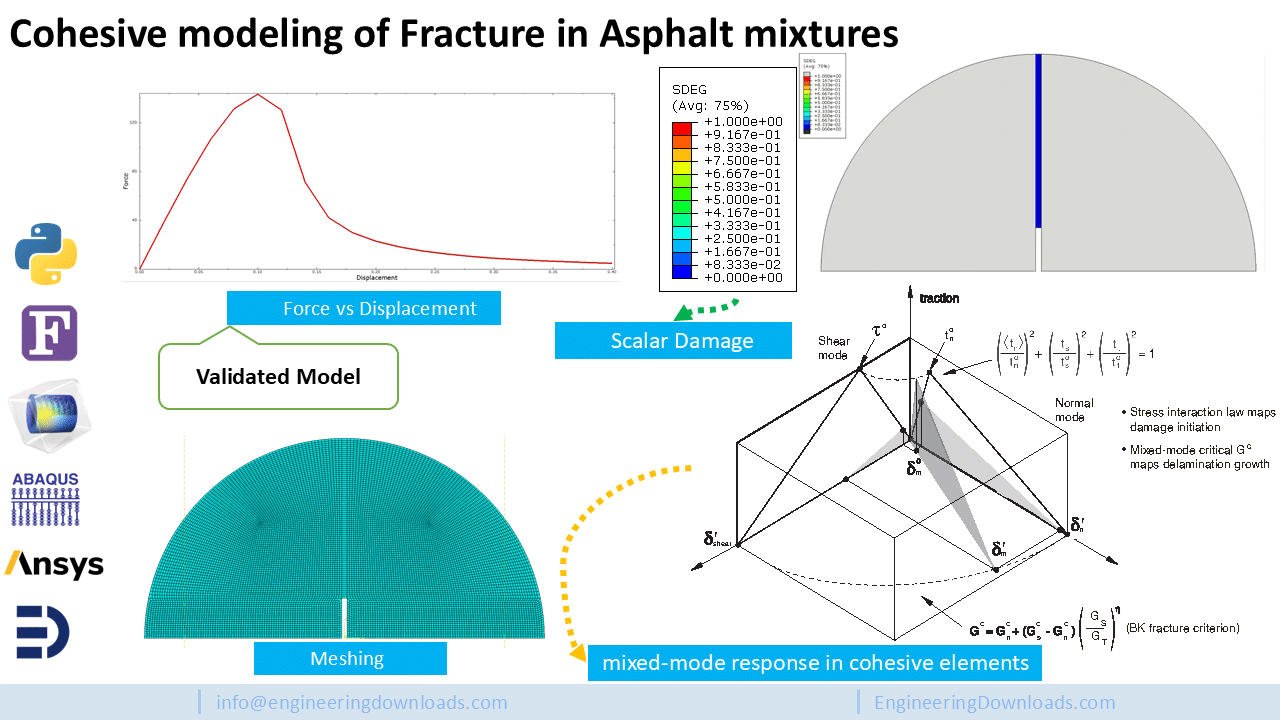
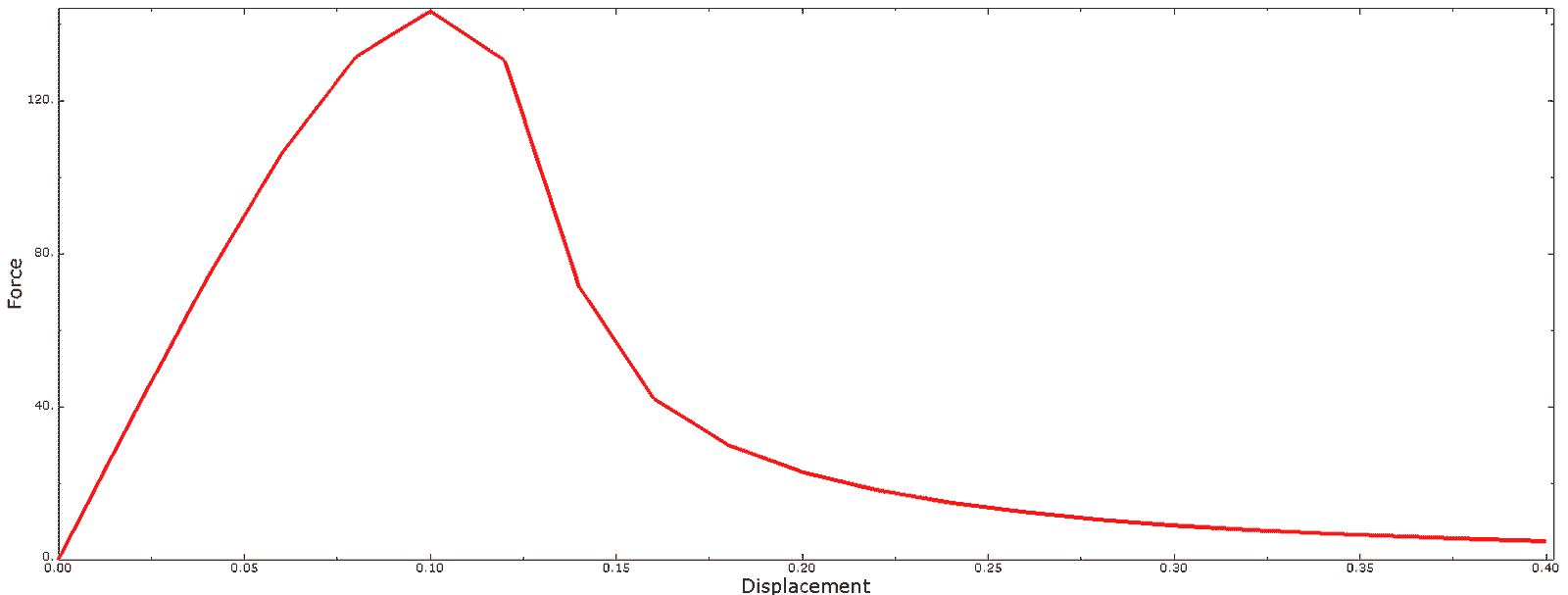
Low temperature cracking is the major distress observed in asphalt pavements in the northern US and Canada. In the past years fracture mechanics concepts were introduced to investigate the fracture properties of asphalt mixtures at low temperatures. In this paper the cohesive zone model (CZM) is used to describe the fracture behavior of asphalt mixtures at low temperatures and the interface element is used to numerically simulate the material response under monotonic loading. The simulation is calibrated with the experimental results from a newly proposed semi circular bend (SCB) test. A parametric analysis of the input material properties indicates that the tensile strength has a significant effect on the peak load in the SCB configuration, the modulus has a strong effect on the calculated stiffness of the SCB specimen, and the fracture energy influences the post-peak behavior of the asphalt mixtures. The calibrated numerical model was applied to simulate the low temperature cracking in a simplified asphalt pavement and to study the influence of these material parameters on the performance of asphalt pavements.

Product description 

This product is a replicated Abaqus implementation of “Cohesive modeling of fracture in asphalt mixtures at low temperatures” (Li & Marasteanu, 2005). It contains the ready-to-run Abaqus files used to reproduce the semi-circular bend (SCB) simulation and the calibrated cohesive-zone implementation reported in the paper.

Material theory & cohesive zone model 

• The models use a Cohesive Zone Model (CZM) implemented with zero-thickness interface elements to localize fracture ahead of the notch/crack.

• An exponential traction–separation law (Ortiz & Pandolfi form) is used: traction T rises to a peak traction T0T_0T0​ at a critical separation δc\delta_cδc​, and the area under the T–δ curve defines the cohesive (fracture) energy GfG_fGf​.

• Bulk material is modeled elastic (Young’s modulus $E$, Poisson’s ratio $\nu$); fracture response is controlled by T0T_0T0​, GfG_fGf​ and the chosen T–δ shape.

• The implementation includes calibration parameters (peak traction multiplier, Gf, mesh/interface placement) to reproduce the experimental load–LLD (load–load line displacement) curves.