

This course provides a comprehensive exploration of biomechanics applied to orthopedic and dental contexts, with a focus on the mechanical principles that govern biological tissues and medical devices. Students will engage with a series of practical, simulation-based examples that bridge theoretical concepts with real-world applications in clinical engineering.
The curriculum is structured to progressively build understanding, starting with fundamental flow and material models before advancing to bone mechanics and implantology. Key topics include:
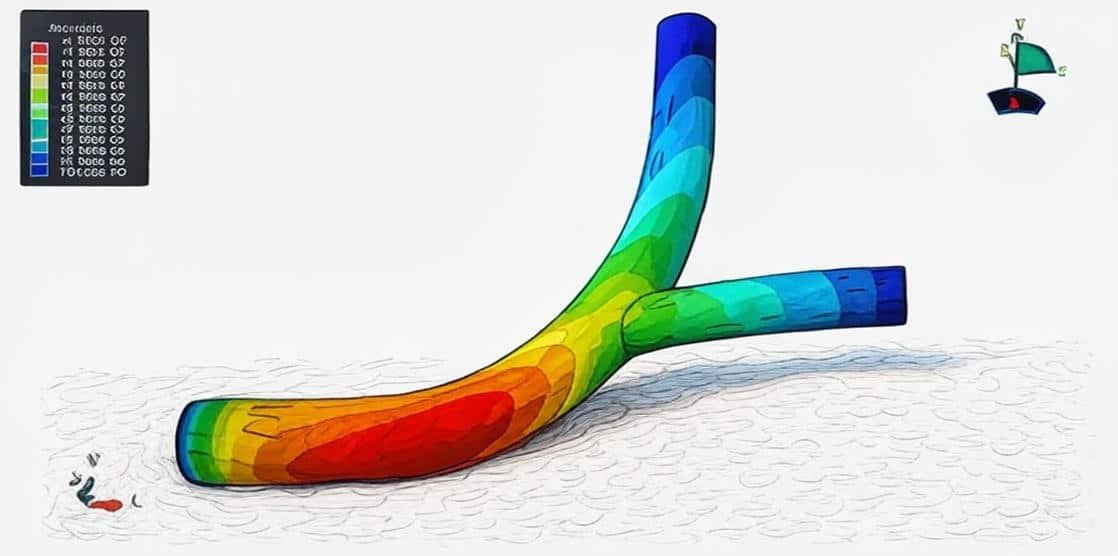
Fluid and Tissue Mechanics: Understanding non-Newtonian models such as Newtonian blood flow and transport phenomena.
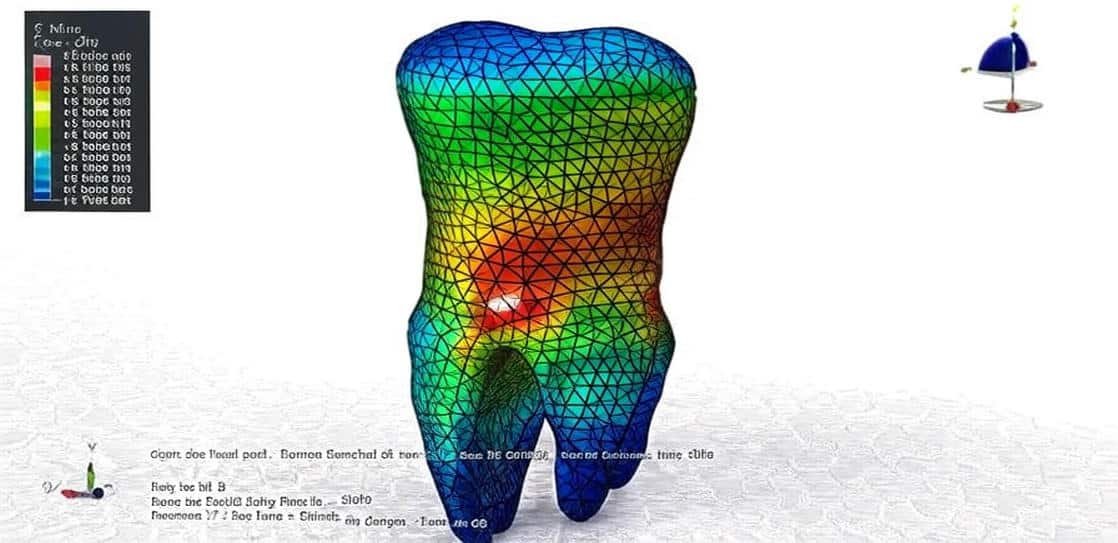
Bone Mechanics and Failure: Analyzing bone structure under cutting, drilling, and cracking scenarios to study mechanical resistance and fracture patterns.
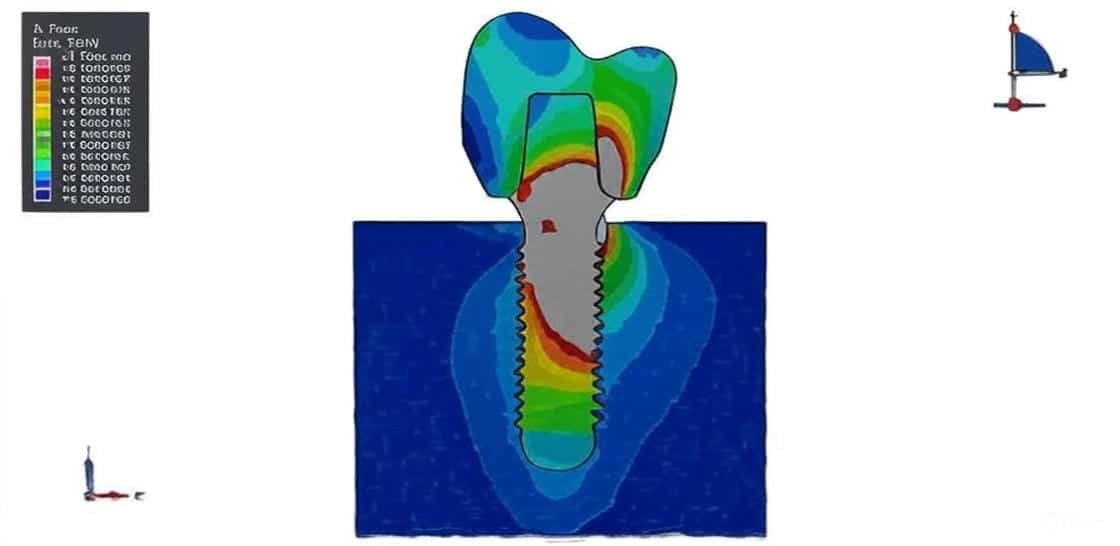
Dental and Orthopedic Applications: Investigating implant insertion, pull-out forces, and static loading on teeth and bone.
Advanced Implant Design: Evaluating porous structures such as TiFoam implants and their interaction with bone for optimized fixation and osseointegration.
Through these modules, students will gain the ability to simulate, analyze, and interpret biomechanical systems, strengthening their understanding of the interface between engineering design and biological function. The course emphasizes practical problem-solving skills and prepares learners to contribute to innovation in medical devices, surgical planning, and clinical biomechanics research.


Abaqus
€81,00 €39,00

Abaqus
€299,00 €249,00

Uncategorized
€95,00 €80,00
Abaqus
€79,00 €38,00
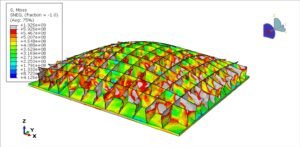
Abaqus
€68,00 €34,00
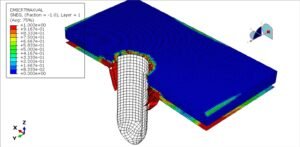
Abaqus
€77,00 €39,00
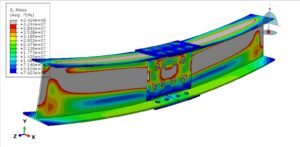
Abaqus
€79,00 €39,00
See more

Want to receive push notifications for all major on-site activities?