Fatigue life estimation is critical in engineering applications where components endure alternating stresses over time. This tutorial explores how Goodman and Gerber correction methods are used to estimate fatigue life for a rotating shaft, providing a clear understanding of their effectiveness in handling different mean stress scenarios.
Stress Analysis (FEM)
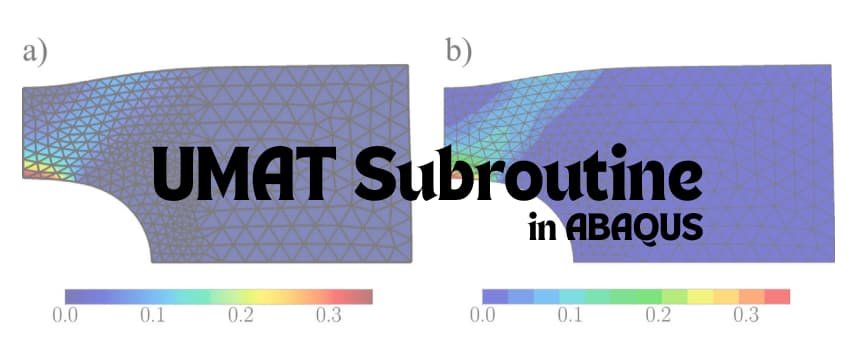
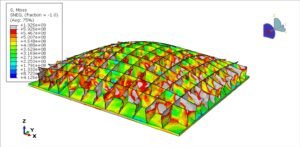
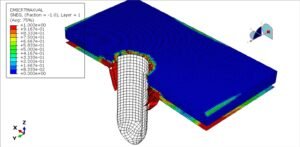
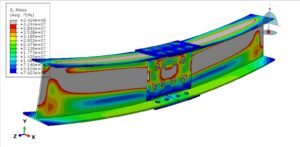
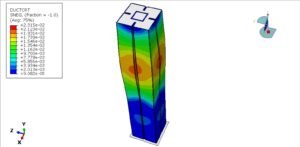
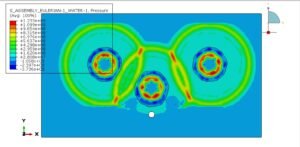
To begin our analysis, we created a finite element model (FEM) of the rotating shaft to evaluate stress distribution. Identifying critical regions based on maximum and minimum stresses lays the groundwork for our fatigue life calculations.
Result: Stress amplitude is σa=200 MPa.
Material Properties for Fatigue Calculations
Understanding the material properties is vital for accurate fatigue life estimation. Here are the key material constants we used for our calculations:
- Ultimate Tensile Strength (Su): 550 MPa
- Fatigue Strength Coefficient (Sf’): Approximately equal to Su
- Fatigue Strength Exponent (b): -0.1
These values are instrumental for calculating the effective stress amplitude ( σa, eff ) and ultimately, the fatigue life.

Effective Stress Calculation Using Goodman and Gerber
Next, we utilize the Goodman and Gerber methods to calculate the effective stress amplitude.
Goodman Equation:

Gerber Equation:

Key Insight: The Goodman correction method accounts for the sign of mean stresses, while the Gerber correction yields identical results for positive and negative mean stress scenarios.
Fatigue Life Estimation Using Basquin’s Equation
We apply Basquin’s equation to estimate the fatigue life under both mean stress conditions:

This equation takes into consideration the effective stress amplitude and material fatigue properties to estimate the cycles to failure.
Results and Observations

Insights
The Goodman correction effectively distinguishes between positive and negative mean stresses, leading to differing predictions in fatigue life estimations. In contrast, the Gerber method offers identical fatigue life estimates for both cases, highlighting its limitations.
Fe-safe: The Software Behind the Analysis
For our analysis, we utilized Fe-safe, an industry-leading fatigue analysis software integrated with finite element analysis (FEA). Fe-safe enables precise fatigue life predictions under various loading conditions.
Key Features:
- Multiaxial fatigue analysis for different materials
- Advanced mean stress corrections
- Seamless integration with FEA tools like Abaqus
Why Fe-safe Matters: This software is crucial for accurate, real-world fatigue life predictions, allowing engineers to optimize designs for safety and performance.
Conclusion
In conclusion, the Goodman correction is more suitable when the sign of mean stress impacts fatigue life, while the Gerber correction fails to capture this distinction, leading to identical results. Understanding these methods is vital for engineers dealing with cyclic loading.
About the Author
This post was written by Saman Hosseini, an expert in fatigue estimation and analysis using Fe-safe. With extensive teaching experience, Saman provides guidance to help engineers effectively use advanced tools for accurate fatigue predictions.
Free Online Consultation
Saman offers free online consultation sessions on fatigue analysis and Fe-safe software. Whether you are a student, researcher, or practicing engineer, you can gain valuable insights tailored to your needs.
📧 To reserve your session, email Saman at: qa@engineeringdownloads.com