Introduction

Arbitrary Lagrangian-Eulerian (ALE) adaptive meshing is a pivotal technique in computational mechanics, effectively blending the advantages of both Eulerian and Lagrangian meshing methods. This hybrid approach is particularly beneficial in Abaqus, a leading finite element analysis software, enabling robust simulations even under severe deformation scenarios. This blog delves deep into the principles of ALE adaptive meshing, its specific applications in Abaqus/Standard and Abaqus/Explicit, and the unique advantages it offers for complex simulations.

Various Meshing Techniques

In computational mechanics, the quality of the mesh can significantly impact the accuracy and efficiency of simulations. There are three primary meshing techniques: Eulerian, Lagrangian, and Arbitrary Lagrangian-Eulerian (ALE).

Eulerian Meshing

Eulerian meshing involves a fixed mesh through which the material flows. This method suits fluid dynamics and problems involving large deformations where tracking specific material points is less critical. Its main advantages include:

• Handling Large Deformations: Effective for scenarios where material interfaces and boundaries change significantly over time.
• Static Mesh: Eliminates mesh distortion issues since the mesh remains fixed.

However, Eulerian meshing has limitations:

• Accuracy in Solid Mechanics: Less accurate for problems involving large displacements or deformations of solid materials.
• Complex Algorithms: Requires sophisticated algorithms to track material interfaces and boundaries effectively.

Lagrangian Meshing

In contrast, Lagrangian meshing involves a mesh that moves with the material. Each node in the mesh attaches to a specific material point, making it ideal for solid mechanics and finite deformations. Key advantages include:

• Natural Conformance: The mesh naturally conforms to the material, simplifying the tracking of material interfaces and boundaries.
• Solid Mechanics: Well-suited for problems involving finite deformations of solids.

However, Lagrangian meshing also has its drawbacks:

• Mesh Distortion: Can become highly distorted in cases of large deformations, leading to numerical inaccuracies and the need for frequent remeshing.
• Fluid Flow Limitations: Not well-suited for fluid flow problems involving large-scale movements.

Arbitrary Lagrangian-Eulerian (ALE) Meshing

ALE meshing is a hybrid approach that combines features of both Eulerian and Lagrangian methods. In ALE, the mesh can move independently of the material, allowing for dynamic adjustment to minimize distortion while still partially following the material. This method offers several advantages:

• Versatility: Combines the strengths of both Eulerian and Lagrangian approaches, making it suitable for a wide range of problems, including fluid-structure interactions and large deformations.
• Mesh Quality: Helps maintain mesh quality and accuracy over time by reducing excessive mesh distortion.
• Flexible Mesh Movement: Can be optimized for specific problem characteristics.

However, ALE meshing is more complex and computationally intensive compared to purely Eulerian or Lagrangian methods. It requires sophisticated algorithms for mesh movement and re-meshing to balance accuracy and computational efficiency.

ALE Adaptive Meshing in Abaqus

ALE adaptive meshing is extensively used in Abaqus to handle complex simulations involving large deformations and material removal. The implementation and functionality of ALE adaptive meshing differ between Abaqus/Standard and Abaqus/Explicit, each catering to specific types of problems.

ALE Adaptive Meshing in Abaqus/Standard

In Abaqus/Standard, ALE adaptive meshing is limited but highly effective for particular applications:

• Fixed Material Domains: Used when no material flows into or out of the domain, such as in Lagrangian approaches.
• Ablation and Wear: Suitable for modeling scenarios where material is eroded at the boundary, like ablation or wear, ensuring high mesh quality under severe deformations.
• Acoustic Analyses: Enables the acoustic mesh to follow significant geometric changes in the acoustic domain due to structural preloading.

A key limitation in Abaqus/Standard is that ALE adaptive meshing cannot create or destroy elements, which restricts its ability to handle extreme deformations.

ALE Adaptive Meshing in Abaqus/Explicit

Abaqus/Explicit offers more comprehensive ALE adaptive meshing capabilities, making it suitable for a broader range of problems:

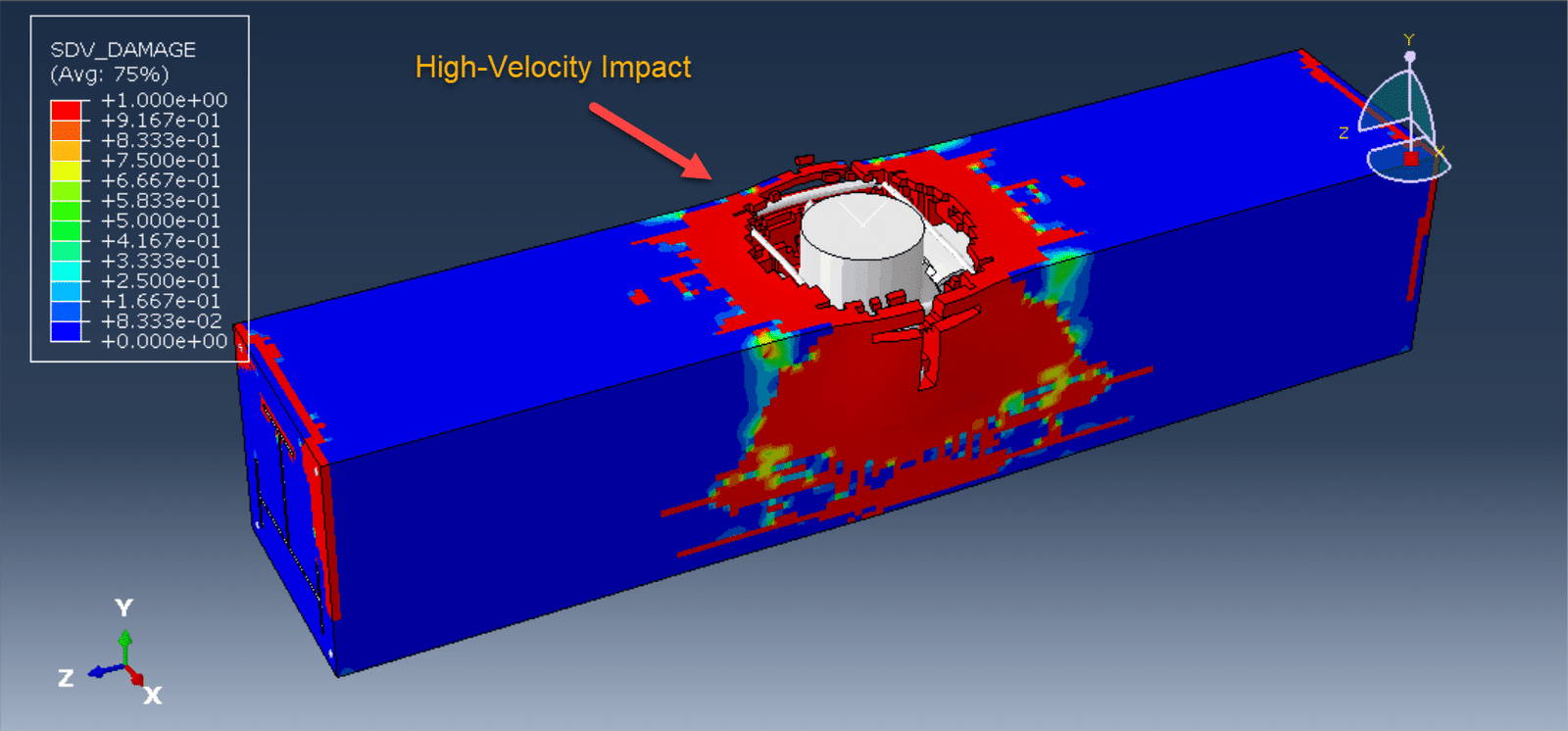
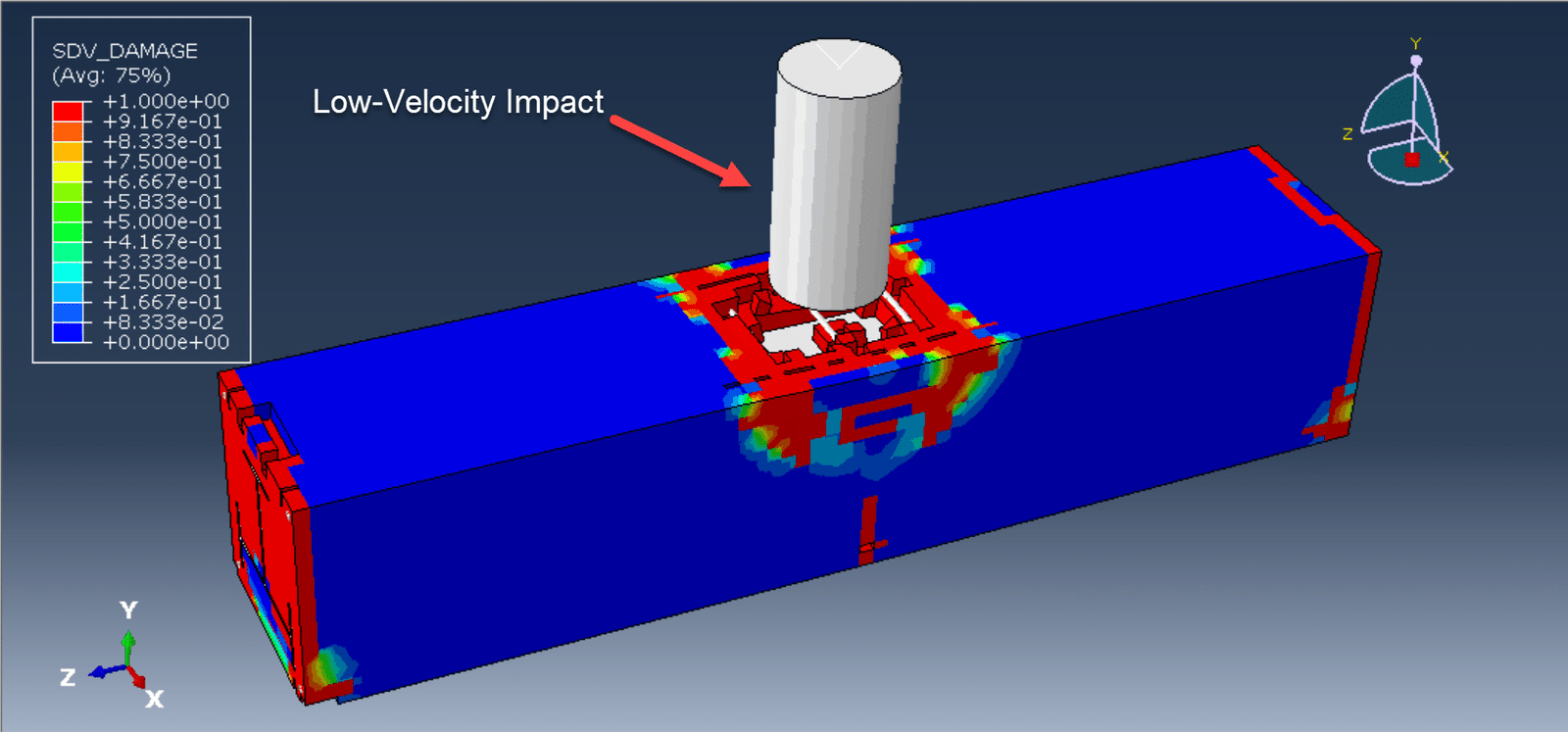
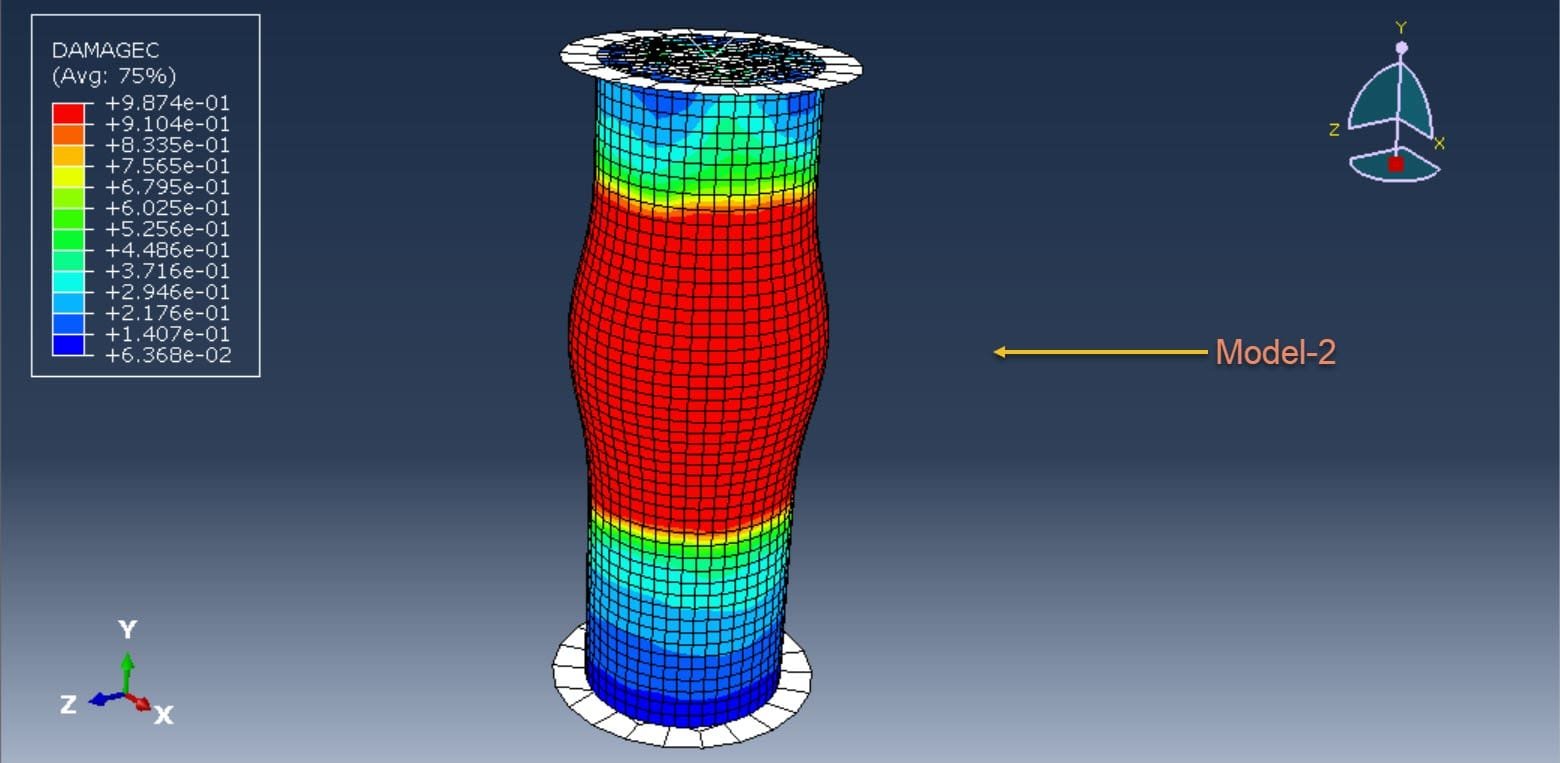
• Large Deformations: Ideal for transient analysis problems undergoing large deformations, such as dynamic impact, penetration, and metal forming processes like forging, extrusion, and rolling.
• Eulerian Problems: Can simulate scenarios where material flows into or out of the mesh, enhancing the accuracy of fluid-structure interaction analyses.
• Steady-State Processes: Useful for modeling steady-state processes and the transient phase in steady-state processes.

ALE adaptive meshing in Abaqus/Explicit includes various smoothing methods tailored for different problem classes, improving the mesh quality before deformation begins and enabling more robust and accurate solutions.

Future Techniques: Adaptive Remeshing and Mesh-to-Mesh Solution Mapping

The techniques of adaptive remeshing and mesh-to-mesh solution mapping will be covered in future sections. These methods are used to enhance mesh accuracy and manage mesh distortions, respectively. Both approaches require specific setups and criteria to ensure effective implementation. Detailed explanations and step-by-step guides for using these techniques in Abaqus/Standard will be provided later in the tutorial.

Conclusion

ALE adaptive meshing in Abaqus is a powerful tool for handling complex simulations involving large deformations and material interactions. By combining the strengths of Eulerian and Lagrangian methods, ALE adaptive meshing ensures high-quality meshes and accurate results. Whether in Abaqus/Standard for fixed material domains and wear modeling or in Abaqus/Explicit for dynamic, large-deformation problems, ALE adaptive meshing enhances the robustness and precision of computational mechanics analyses.