Product Overview:

This tutorial delves into the simulation of three-dimensional fatigue phenomena in Abaqus, employing Paris law to model crack growth. Metal fatigue is a process where materials gradually degrade under stresses and strains that are lower than the levels required for immediate failure. For instance, consider a steel wire used to suspend weights that do not exceed its tensile strength. Over time, however, these weights can induce the formation of defects in the steel, which may manifest as scratches, notches, or other imperfections. Eventually, these defects can accumulate to the point where the steel wire breaks, despite never having experienced stress beyond its tensile strength.

The process of metal fatigue varies significantly across different materials. In certain instances, defects may appear almost immediately upon the application of stress, growing slowly until total failure occurs. In other cases, no visible damage may be detected until the failure is imminent; then, defects can proliferate rapidly just before complete failure.

Several factors influence the stress or strain required to initiate metal fatigue, commonly known as the fatigue limit or fatigue strength of the material. Key factors include:

1. Material Properties: Typically, the fatigue limit for many materials ranges from one-quarter to three-quarters of their tensile strength.
2. Magnitude of Applied Stress: Higher stress levels generally lead to quicker onset of fatigue.
3. Environmental Conditions: For example, metal submerged in a saltwater solution is likely to exhibit fatigue sooner than a similar piece tested in air. Additionally, oxidized materials tend to experience fatigue more rapidly compared to their unoxidized counterparts.

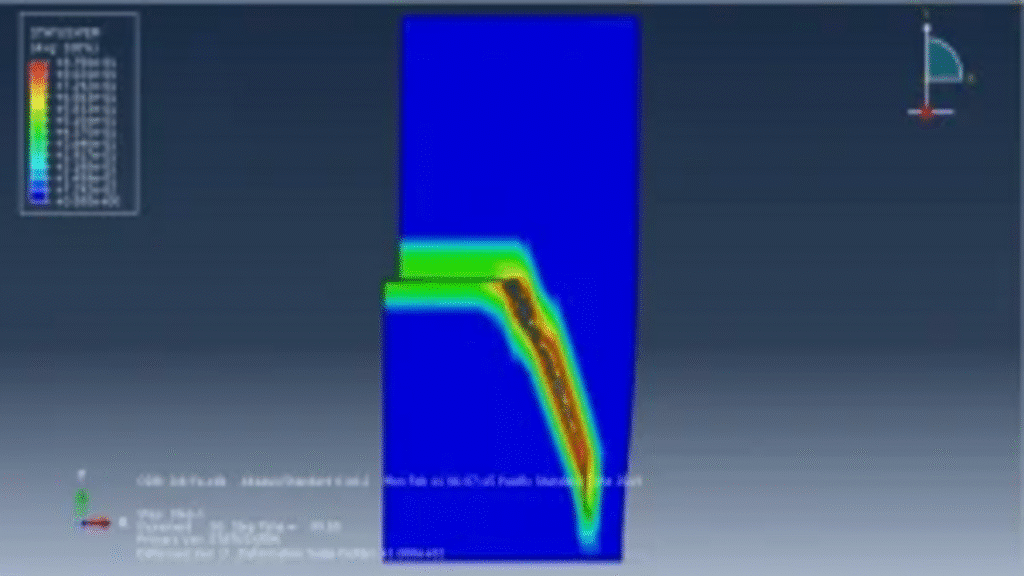
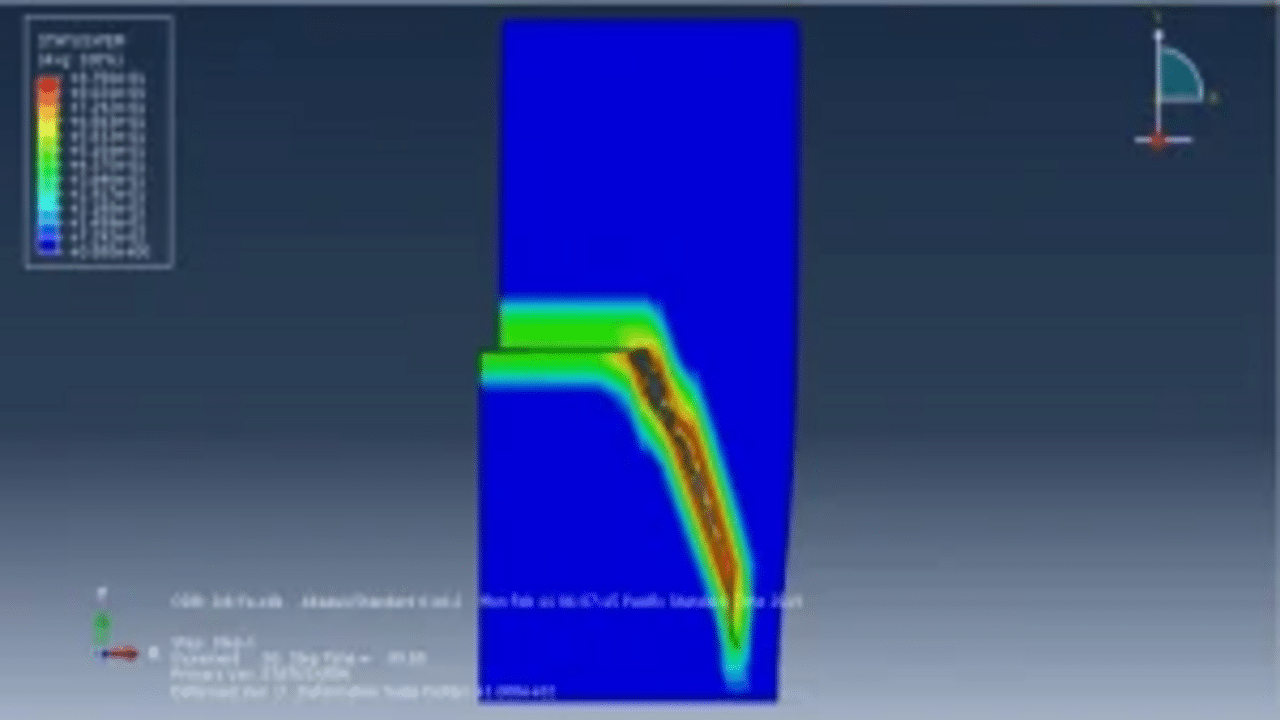
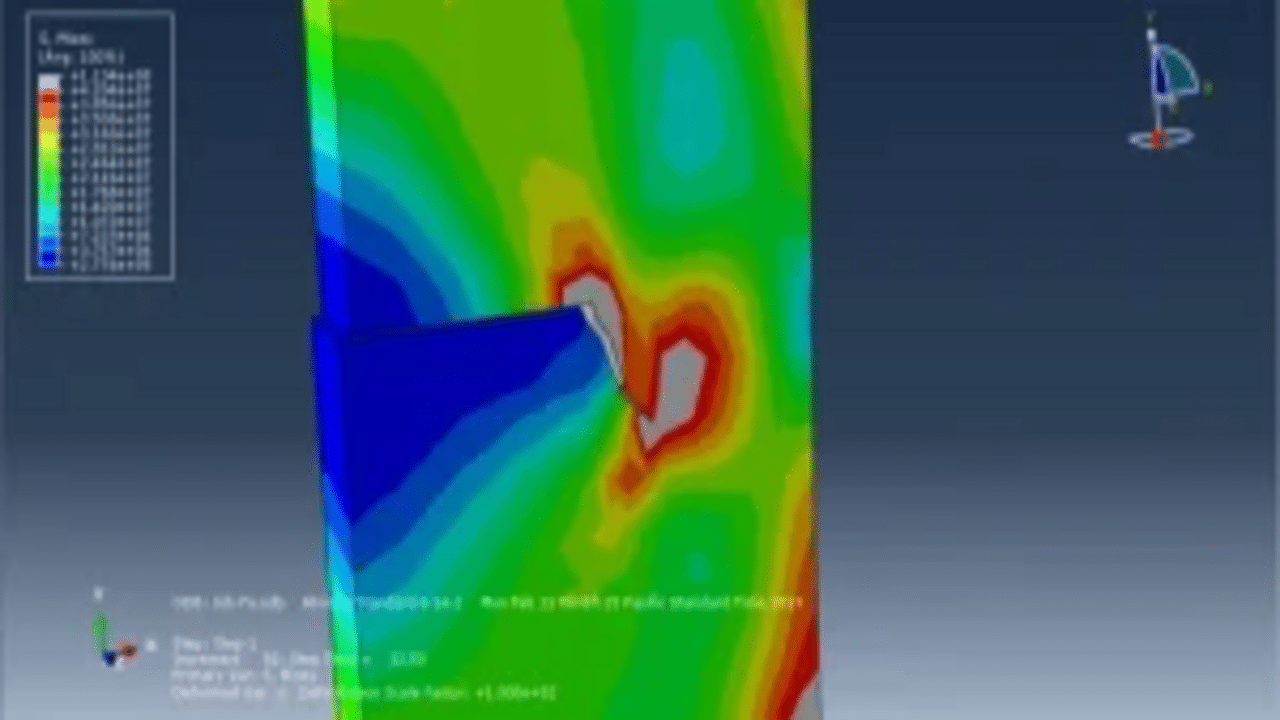
In this simulation, we utilize a solid steel part modeled as an elastic material, combined with a traction-separation law to accurately represent crack growth. A direct cyclic step is employed, with simulations extending to a maximum of one hundred cycles.

To assess fatigue behavior, Paris law is implemented in the input file, along with a power law to define the fracture parameters. Throughout the simulation process, crack growth and fatigue data are readily visualized for each cycle, providing insight into the material’s response under cyclic loading.