
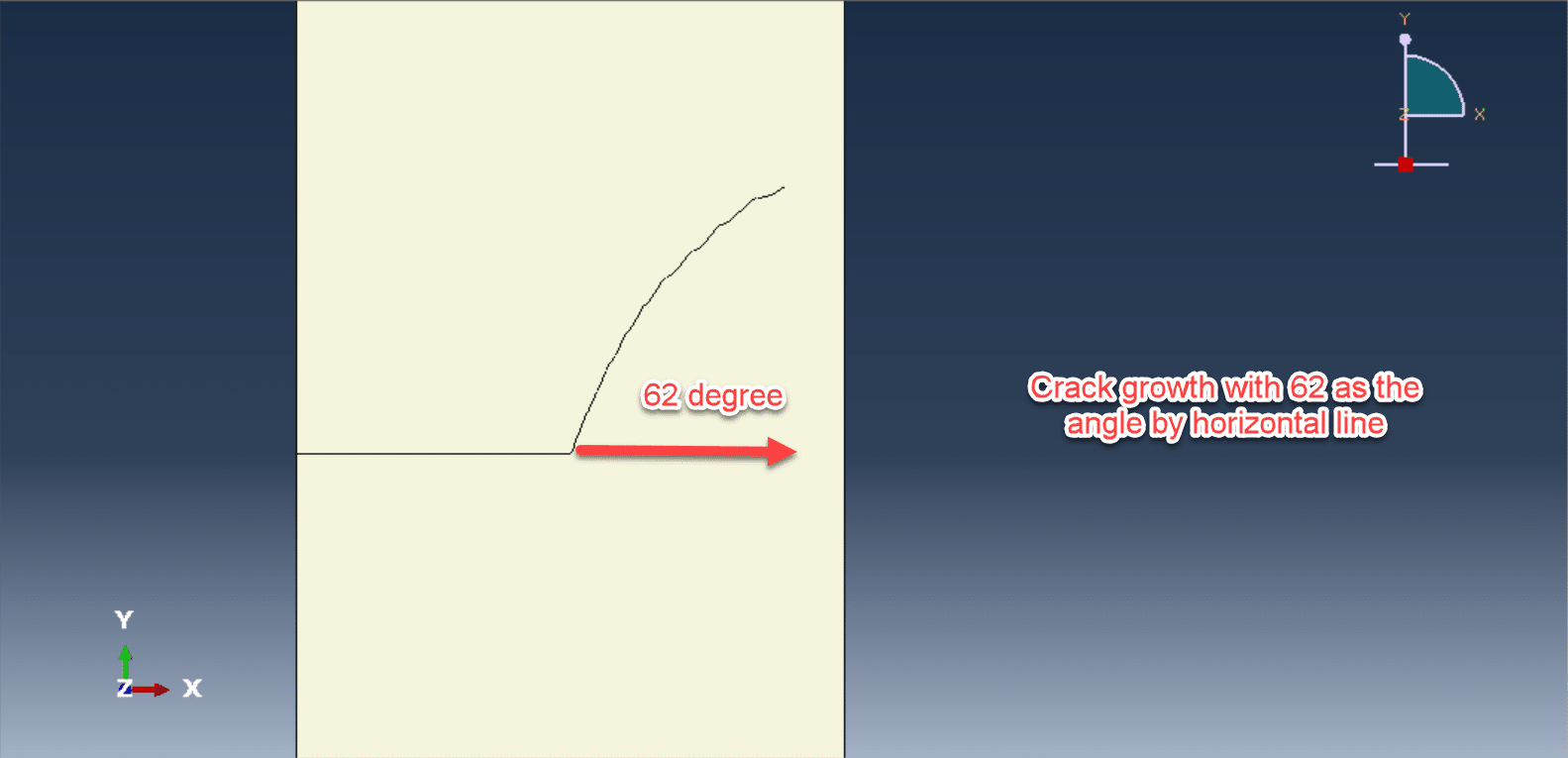
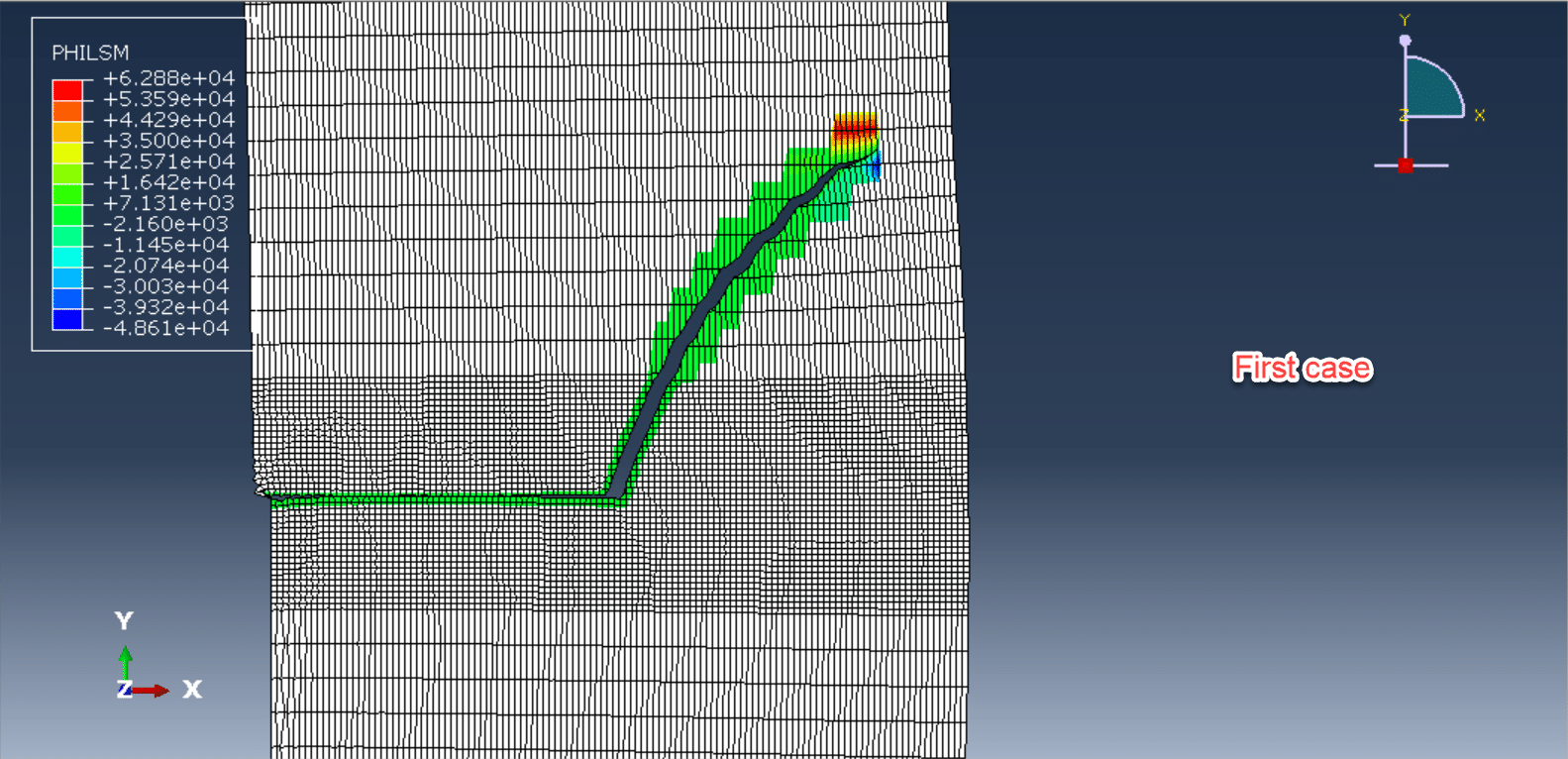

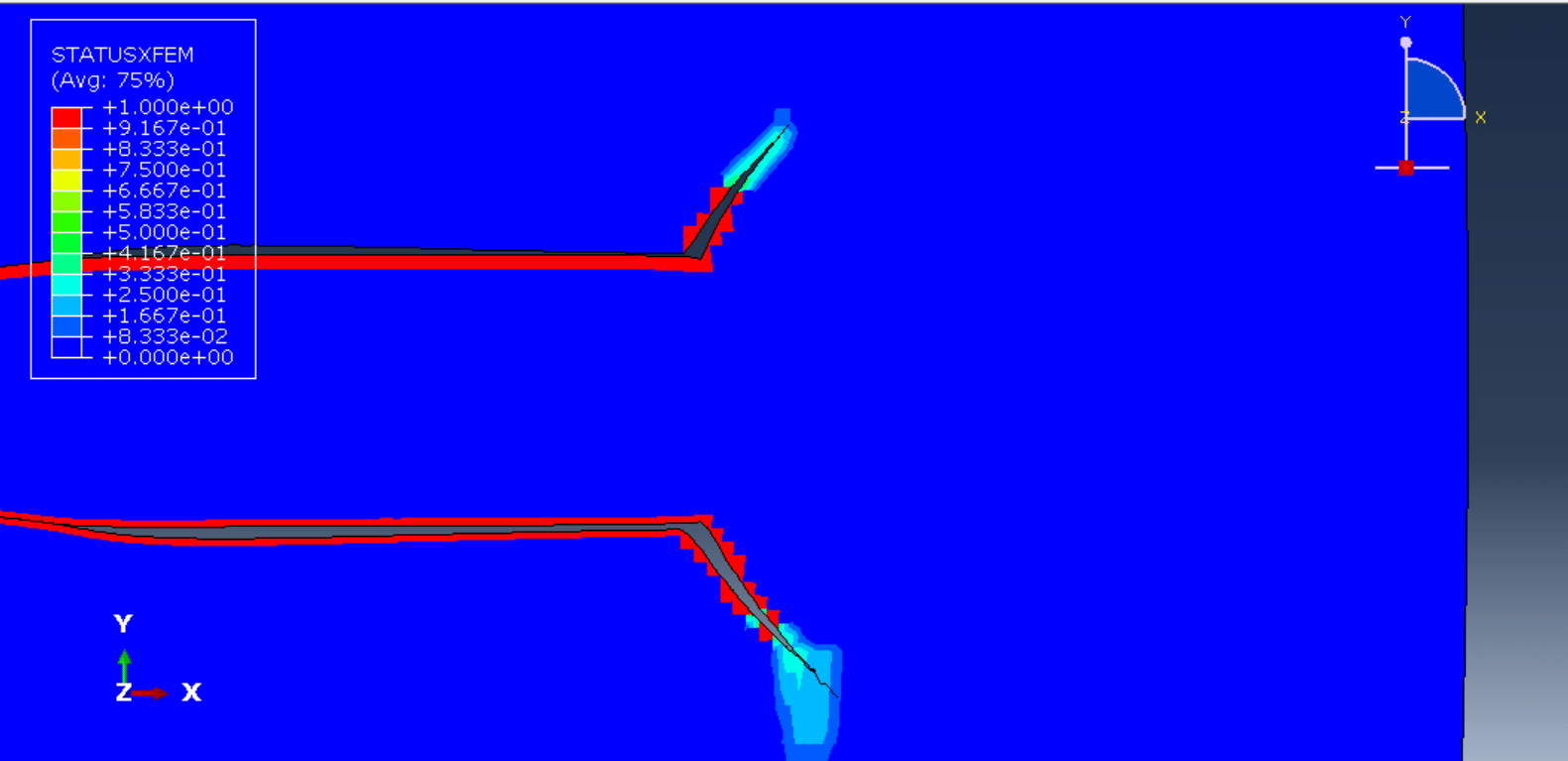

Fracture dynamics under impact loading has long been a central topic in solid mechanics, especially for understanding and predicting crack initiation and propagation in brittle materials. Among benchmark problems for dynamic fracture, the Kalthoff–Winkler experiment is widely recognized for its clear depiction of crack branching and propagation direction under oblique impact conditions. This experimental setup, involving the impact of a steel plate with pre-notched edges subjected to low-velocity loading, has been instrumental in validating fracture criteria and numerical models.
Traditional continuum mechanics approaches based on classical partial differential equations often face challenges in modeling dynamic crack growth, particularly due to their reliance on spatial derivatives, which become ill-defined at discontinuities like cracks. To overcome these limitations, the peridynamic theory, a nonlocal reformulation of continuum mechanics introduced by Silling (2000), has emerged as a powerful alternative. In peridynamics, material points interact with each other through finite-range forces (bonds), allowing for a natural and mathematically consistent treatment of discontinuities and fragmentation without the need for supplementary crack-tracking algorithms.
In this context, peridynamic modeling of the Kalthoff–Winkler experiment under low-velocity impact has become a compelling case study. By capturing the full-field damage evolution and crack path without predefining crack trajectories or insertion criteria, peridynamics provides insights into the initiation time, crack angle, and branching phenomena observed in experiments.
The primary objectives of using peridynamics for the Kalthoff–Winkler setup under low-velocity impact are:
To simulate the dynamic fracture response of notched plates with high fidelity, replicating the experimentally observed crack angles (typically ~70° to the notch direction).
To study the influence of impact velocity, material heterogeneity, and horizon size on the crack growth process.
Overall, the integration of peridynamic theory with classical fracture benchmarks like the Kalthoff–Winkler test provides a robust framework for advancing computational fracture mechanics, particularly in regimes where traditional methods fall short.
Classical finite element methods (FEM) face inherent limitations in capturing crack initiation and complex propagation paths without ad hoc criteria for crack insertion or remeshing. In contrast, peridynamics, a nonlocal continuum theory, addresses these challenges by replacing spatial derivatives with integral operators, allowing for discontinuities (like cracks) to emerge naturally from the governing equations


Acoustic
€100,00 Original price was: €100,00.€99,99Current price is: €99,99.
Abaqus
€150,00 Original price was: €150,00.€120,00Current price is: €120,00.
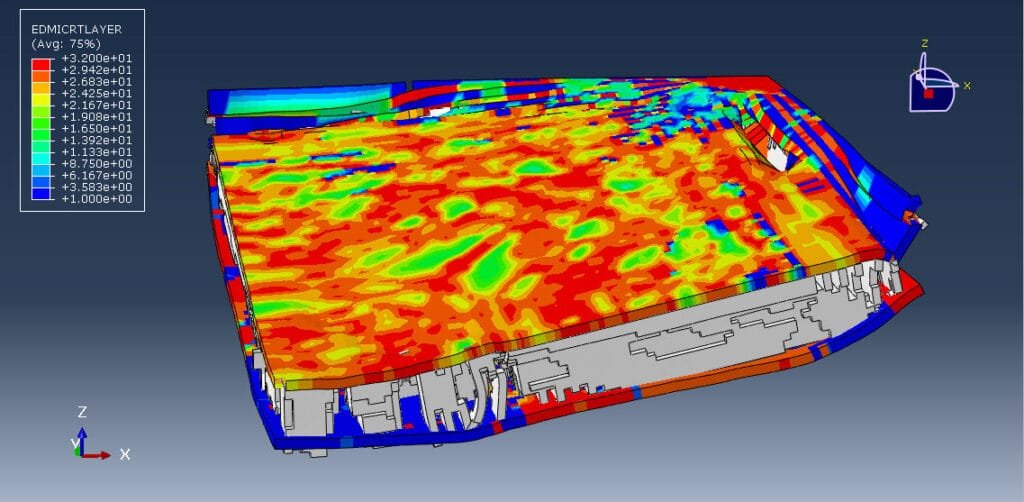
Abaqus
€49,00 Original price was: €49,00.€29,00Current price is: €29,00.
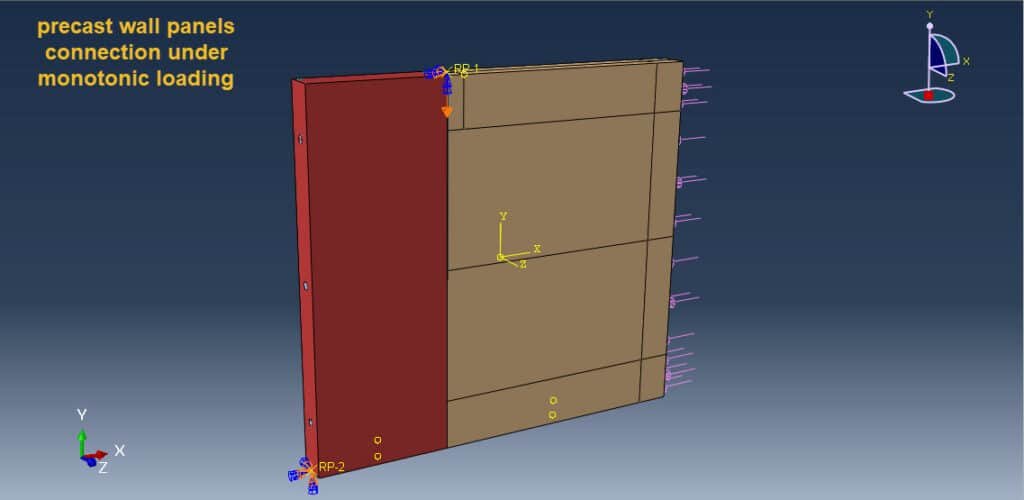
Abaqus
€46,00 Original price was: €46,00.€26,00Current price is: €26,00.

Abaqus
€50,00 Original price was: €50,00.€30,00Current price is: €30,00.
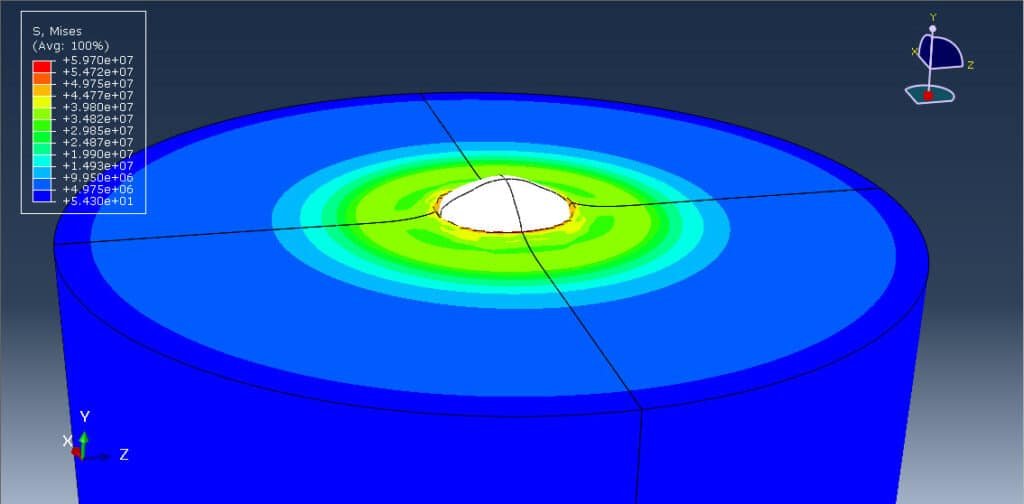
Abaqus
€46,00 Original price was: €46,00.€27,00Current price is: €27,00.

Abaqus
€45,00 Original price was: €45,00.€28,00Current price is: €28,00.
See more
Let’s Learn and Collaborate
Get VIP access to new content.
Sign up for weekly deals and news.
Engineering Downloads is a hub for learning,
collaboration, and sharing engineering models
and resources.
© 2025 Engineering Downloads. All rights reserved.

Want to receive push notifications for all major on-site activities?